4 梯度下降
本文内含大量数学公式,全部采用mathjax渲染。
从理论上来说,我们现在的模型已经可以处理任何分类问题了,接下来我们要解决的是让机器自动调整,达到我们的目的。
这就要请到我们的老朋友Y与y了:
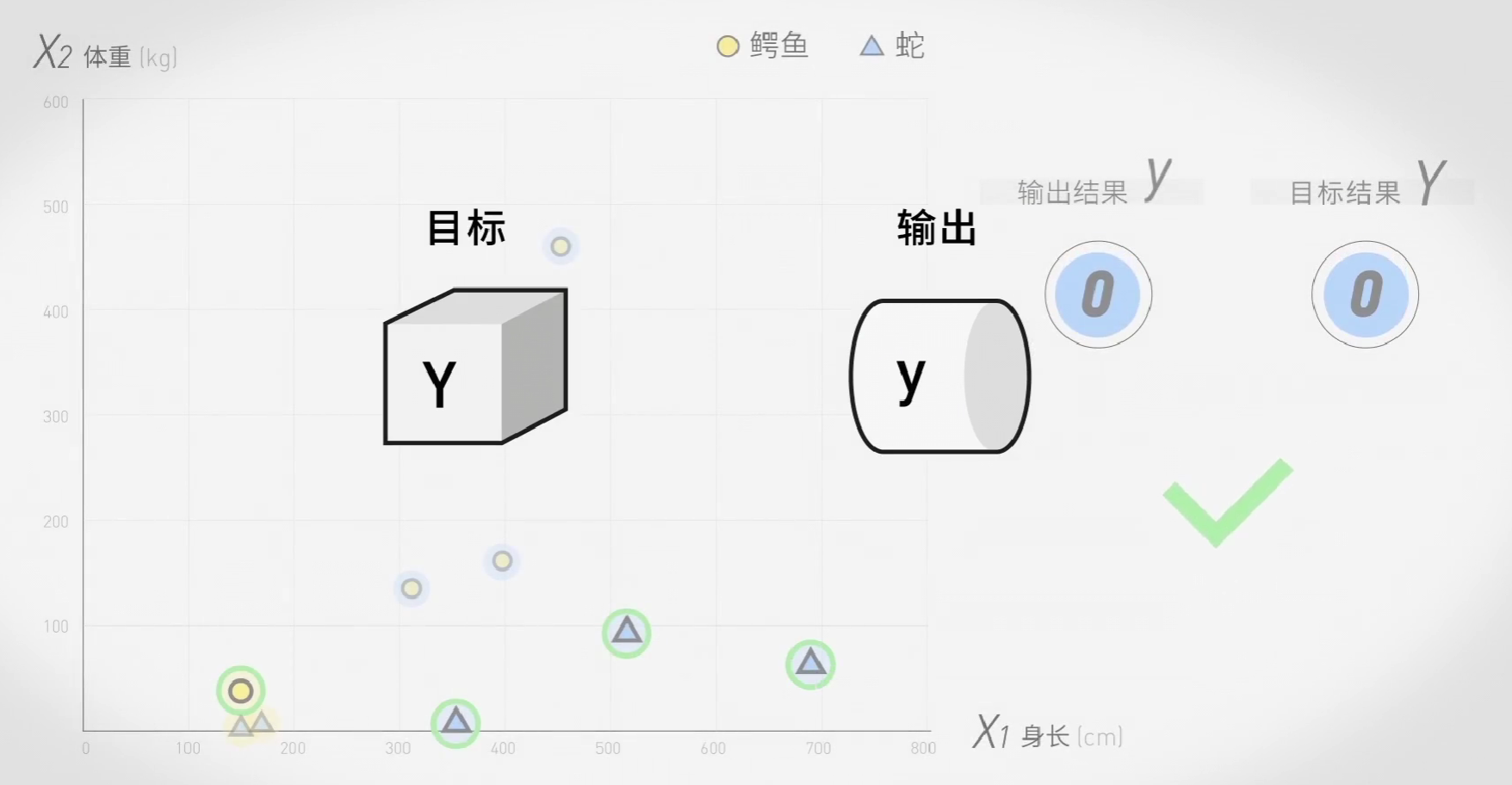
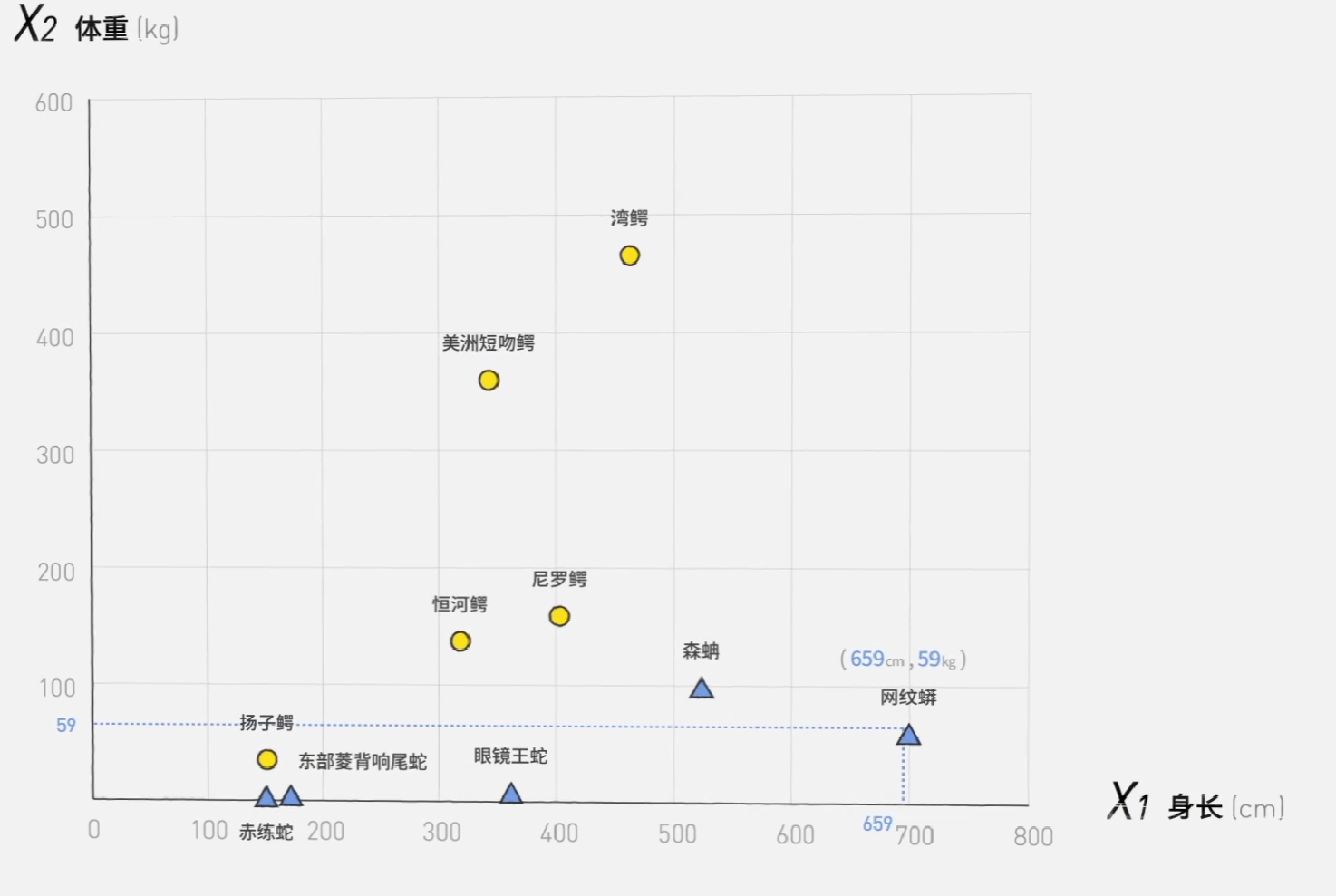
容易想到,输出值y和目标值Y越接近,机器就越准确。
比如说在如下的神经网络中,将所有权重与阈值设置为0,再使用阶跃函数,是所有的输出都为1,通过设定目标值,我们可以得到如下的误差表:
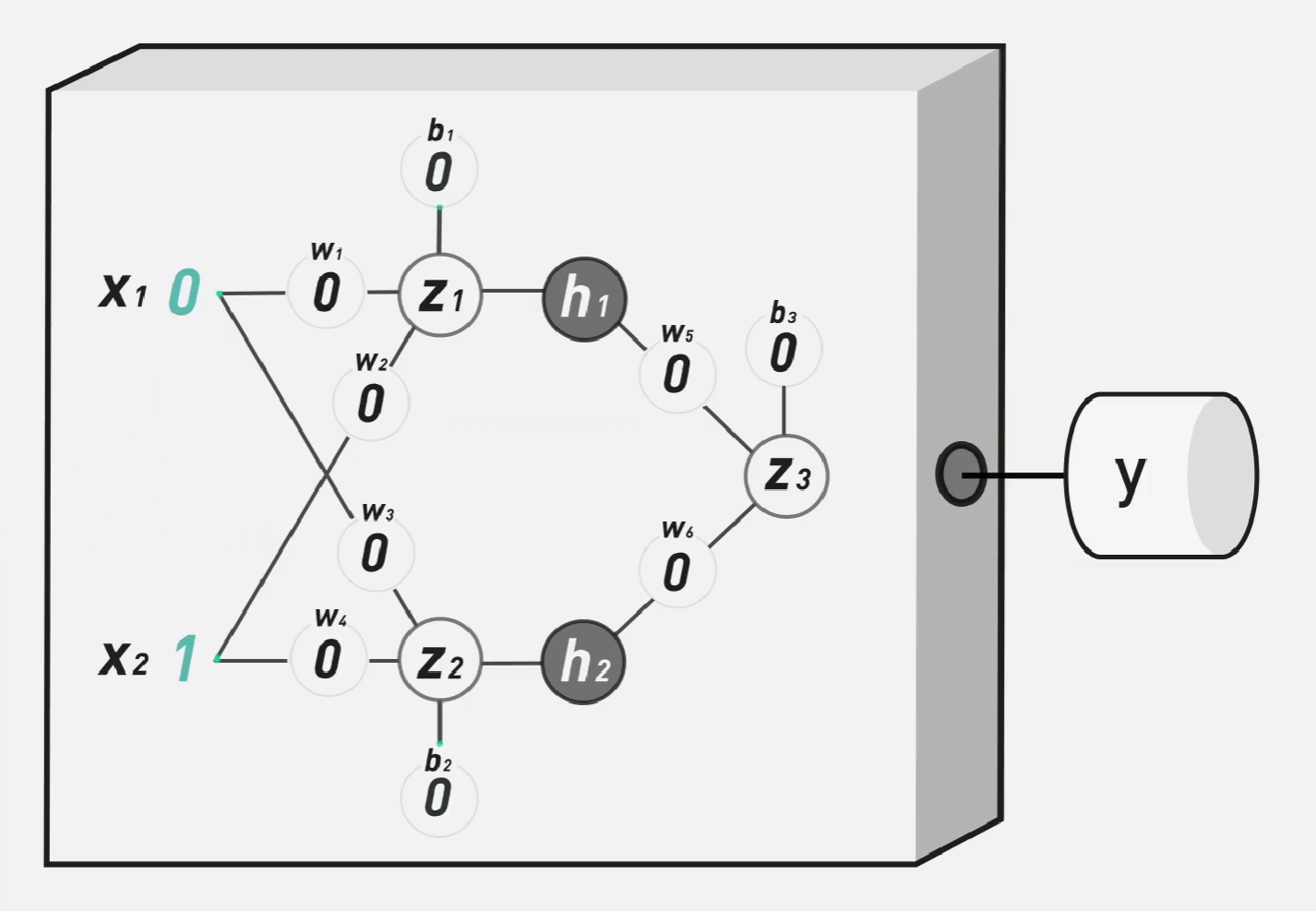
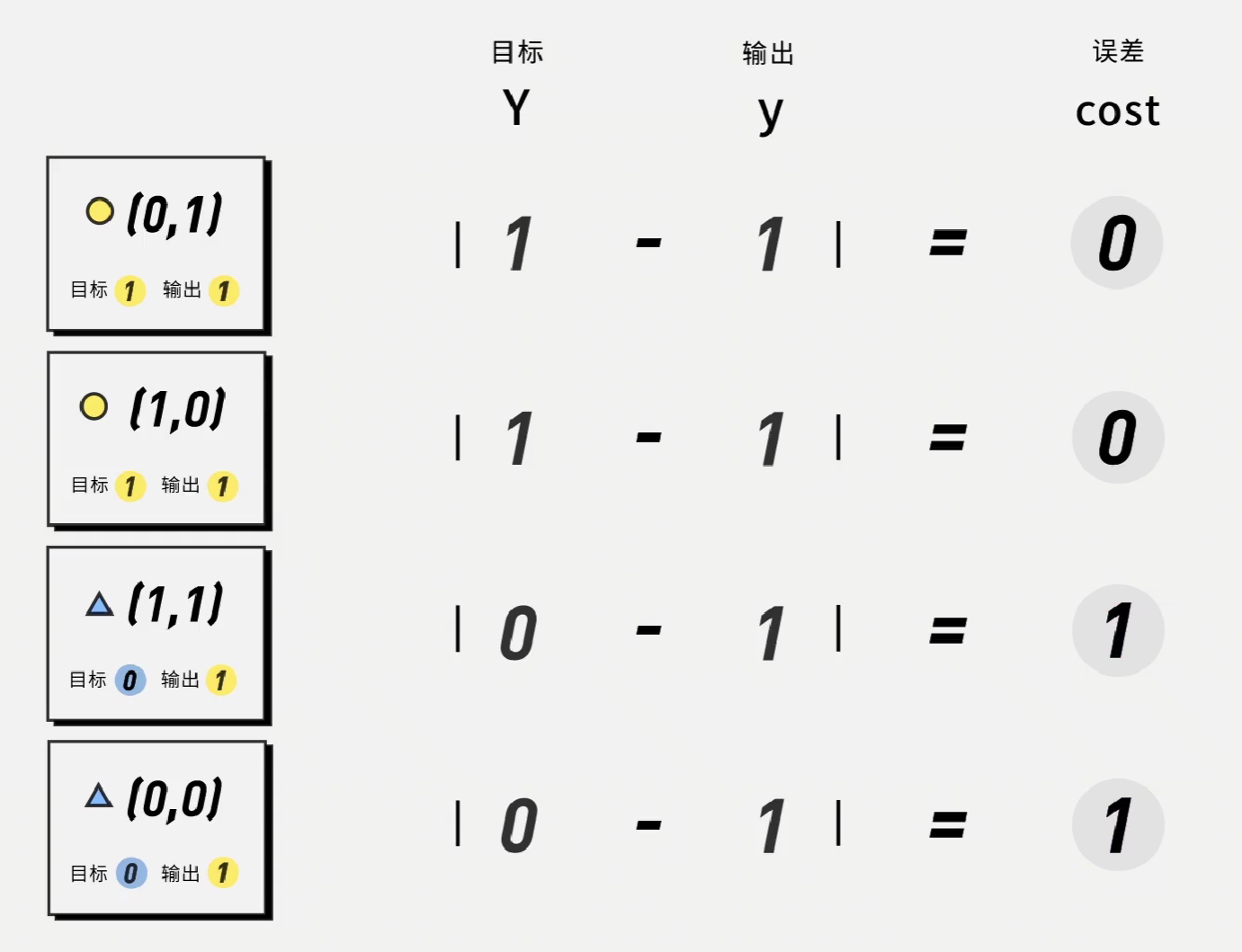
我们定义模型误差,由如下公式计算:
\[cost=\frac{1}{N}\sum|Y-y|\]
误差越低,机器就越准确。在本例中,\[cost=\frac{1}{4}\times(0+0+1+1)=0.5\]
而这个结果受到模型中每一个权重和阈值的影响,这样我们就得到了一个函数,这就是损失函数:
在常见的机器学习模型里,这个结果会平方一下便于计算。
\[Cost = \frac{1}{2N}\sum|Y-y|^2=f(W_1,W_2,W_3,W_4,W_5,W_6,b_1,b_2,b_3)\]
有了损失函数,我们才能给机器一个明确的目标,让损失函数越低越好,再抽象一点就是下山,下一座十维的山。机器需要在这十个方向上爬山,找到最低点。
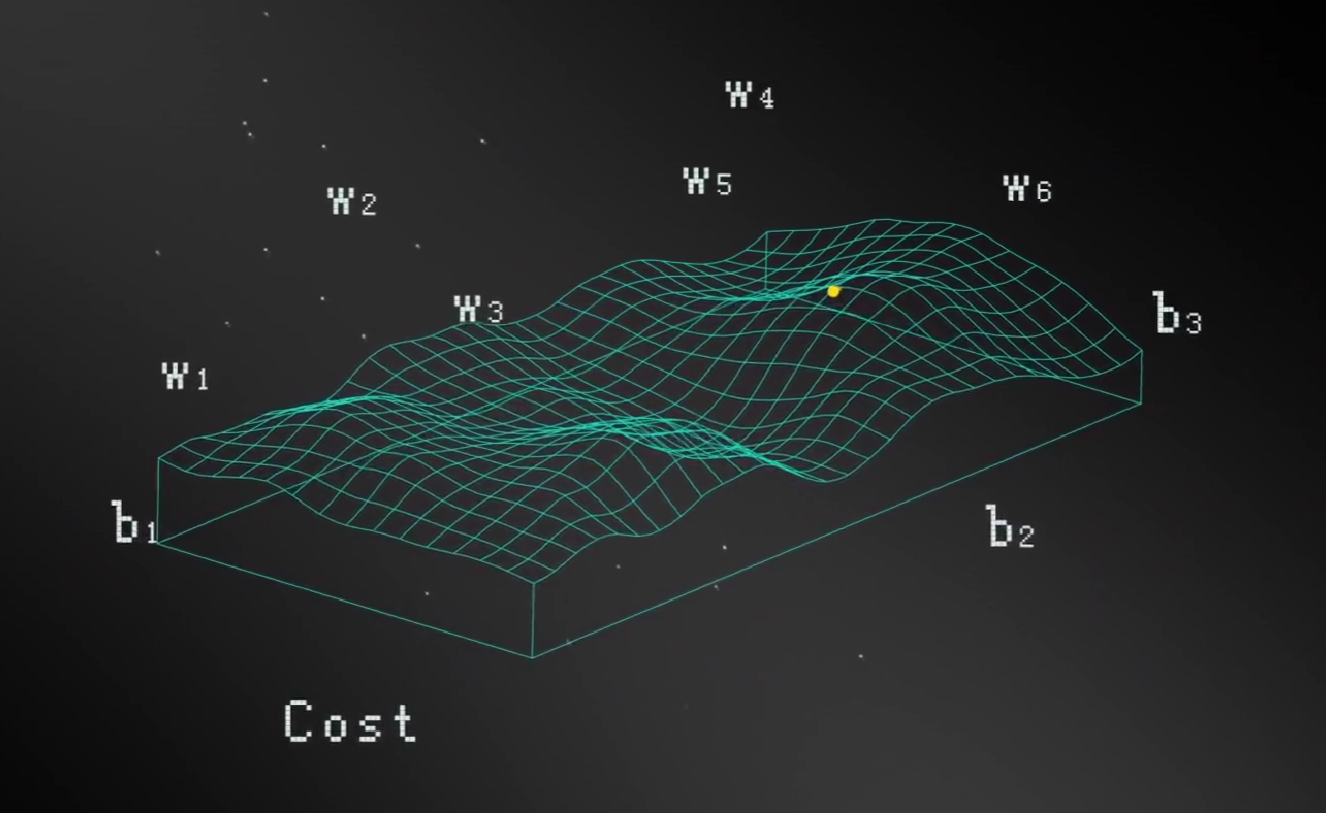
而我们需要找到一个算法,给机器找到下山的路,隆重介绍:梯度下降(Gradient Descent)
顾名思义,梯度下降 = 梯度 + 下降,或者说是下楼梯。我们会先在一个变量的函数中下楼梯,然后逐渐增加到九个变量。
让我们从最简单的函数开始,\(y=x^2\):
我们的目的很简单,对于任意的点都能让它自动寻路,通过调整x走到最低点,也就是y最小的地方。
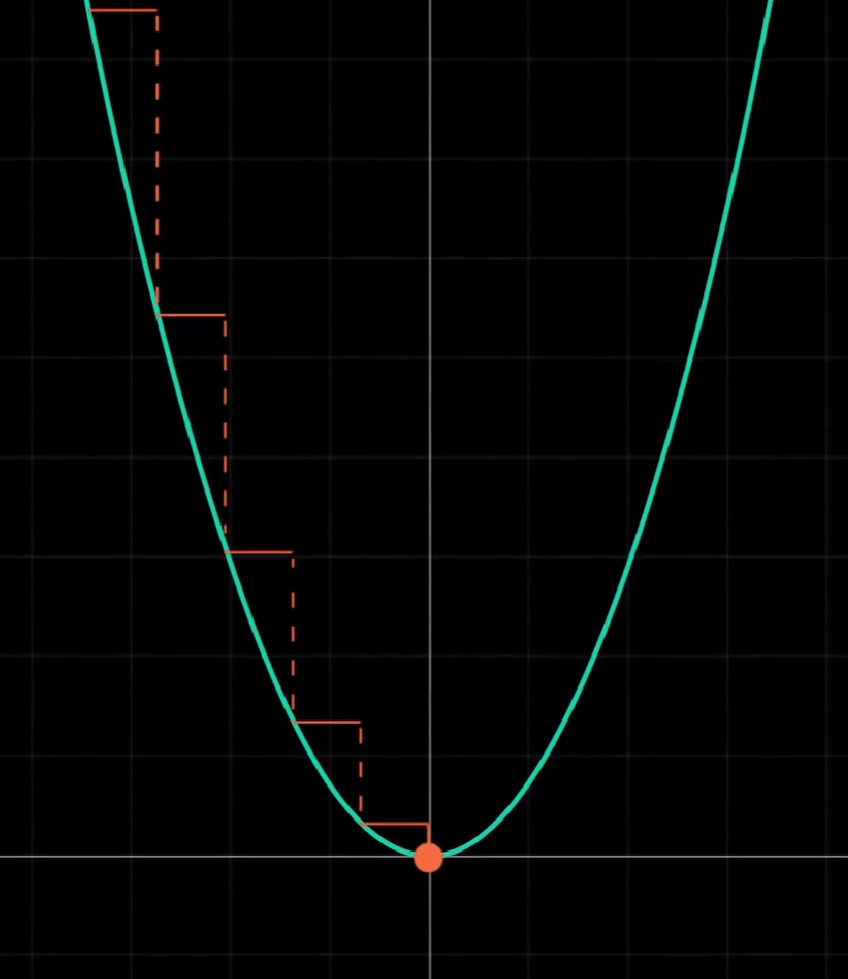
要做到这一点,我们需要掌握两件事:每一步的移动方向和移动距离。即x应该变大还是变小,变大或变小多少。
容易想到,如果该点的切线斜率为负,我们应该让x变大,向右走;如果该点的切线斜率为正,我们应该让x变小,向左走。
然后便是距离,过大会错过最低点,过小会造成较大的时间开销。我们应该做的,是让斜率和移动的距离成正比,在陡峭的地方走多点,在平缓的地方走少一点。
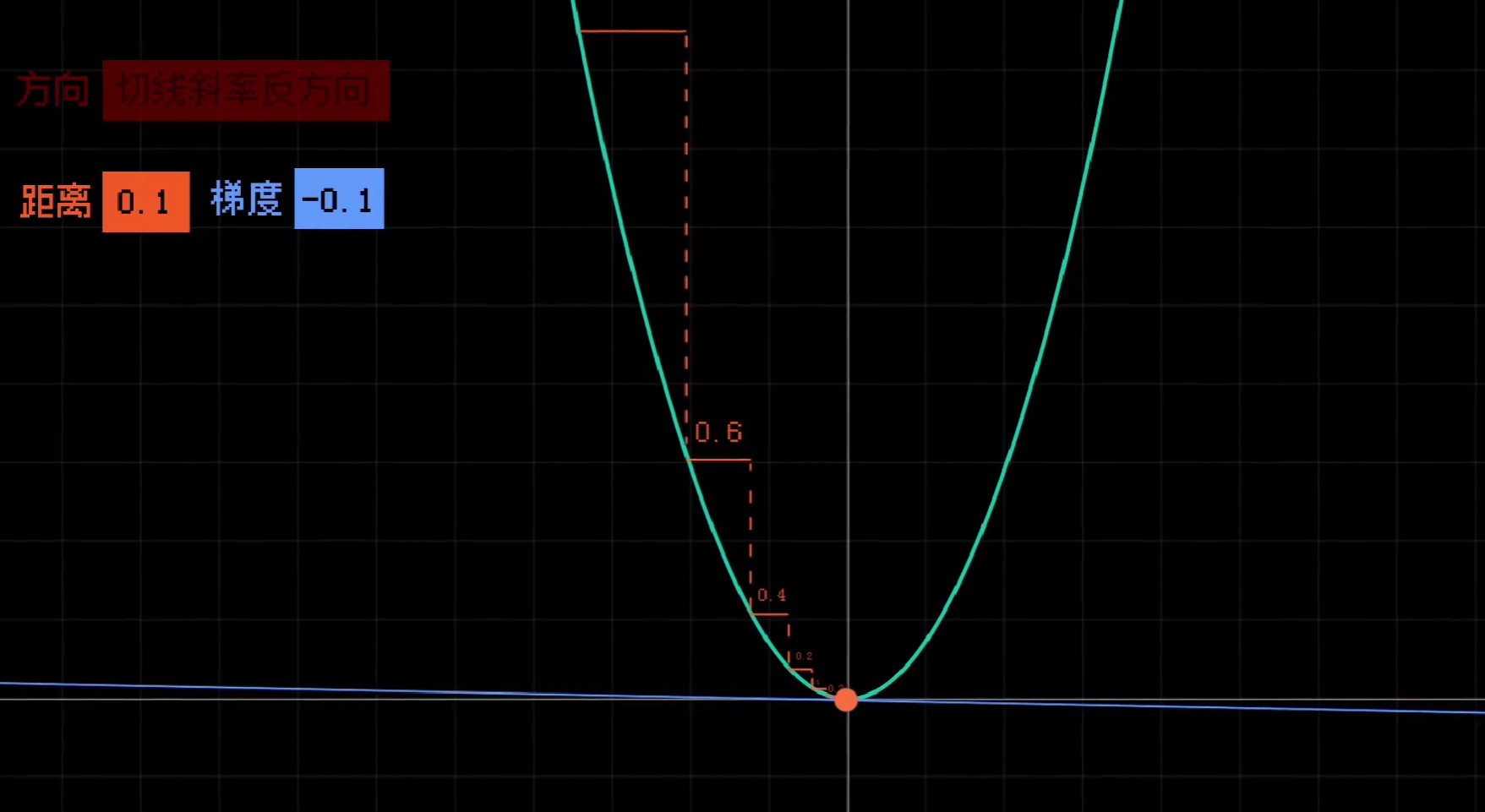
而乘上的这个比例,我们称作步长,也就是我们之前提到过的学习率。
现在我们增加一个变量,令:
\[z=x^2+y^2\]
我们可以得到一个抛物面。现在,我们想让一个小球自由调整x和y,让它走到最低点。

沿用刚才的方法,我们需要找到让z下降最快的大小和方向。我们可以拆解一下这个问题:先让小球分别在x方向和y方向上进行下降:

然后将两个方向进行合成。

就可以让小球下降到最低点。

在这个过程中,求导始终是十分关键的一步,因为导数意为着斜率,即我们的移动方向。
回到我们最开始的问题:我们需要做的,就是求出损失值C对这九个变量的偏导数,让误差值越来越低。
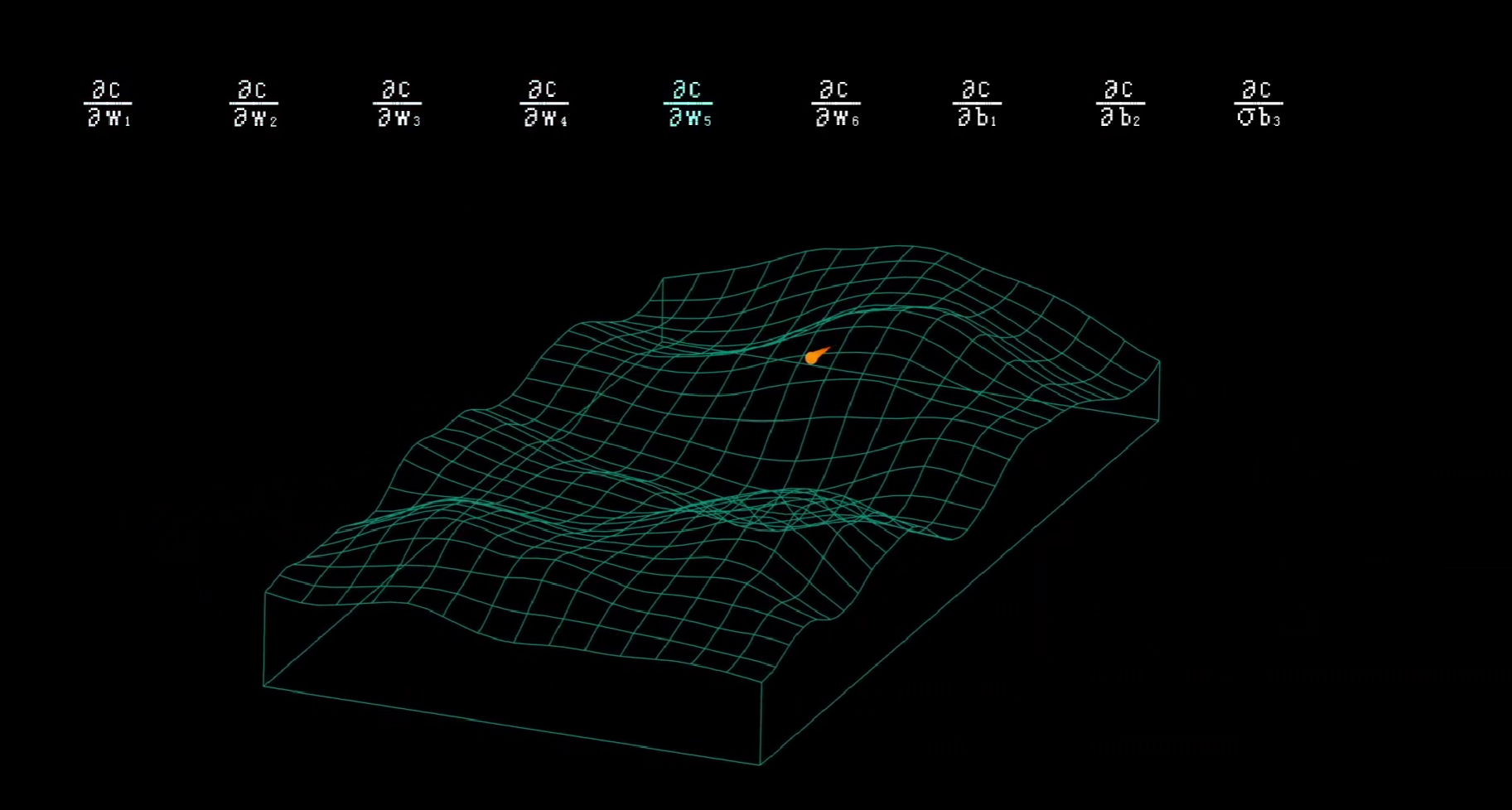
现在,我们只差最后一步了。
如果要求损失函数对九个变量的偏导数,我们首先需要做一些准备工作:
我们可以先给权重和阈值随便设置一下初始值,再来考虑激活函数:
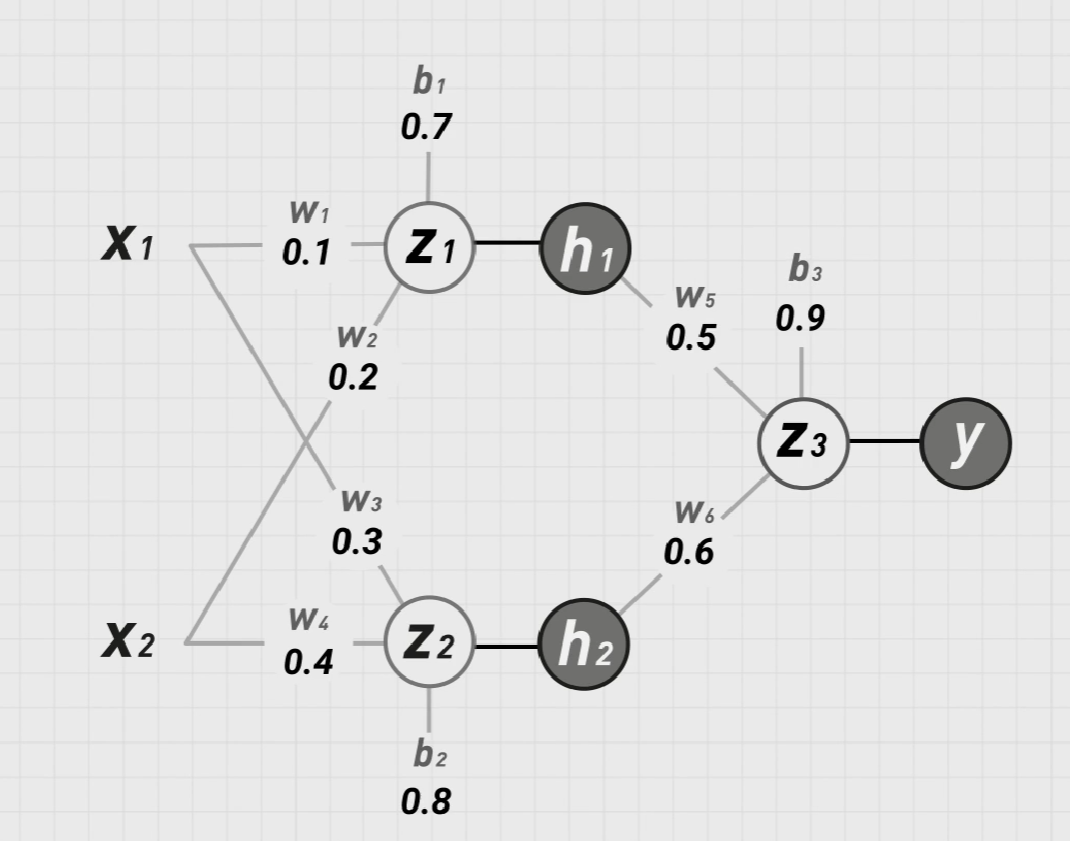
注意:这里不能采用阶跃函数:因为阶跃函数除了原点不可导,其他点的导数为0,无法做梯度下降。我们暂时采用逻辑函数:
\[\sigma (x)=\frac{1}{1+e^{-x}} \]
给定一组输入(1,0)我们就可以填出图中所有的空,并且可以算出他的损失值:
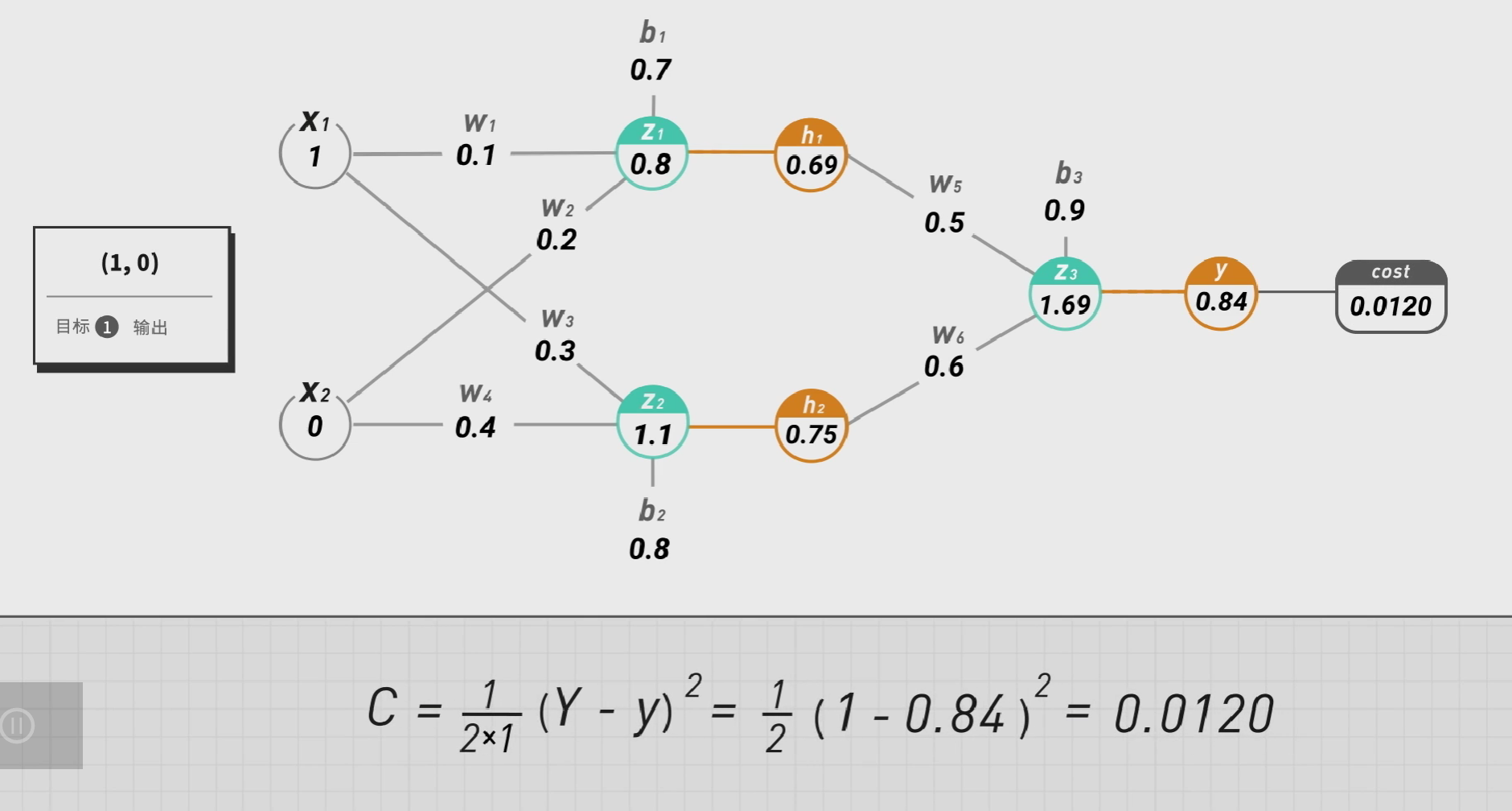
这个过程,我们称之为前向传播(Forward Propagation),即从左往右将训练送入网络以获得激励响应。
与之类似,我们有反向传播(Backward Propagation),即“误差反向传播”的简称,该方法对网络中所有函数计算损失函数的梯度,这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。
从图上来看,就是从损失值C出发来推算W和b要改变的量。具体的做法就是在九个变量上做梯度下降,即求C对九个变量的偏导数。

这就需要用到链式法则来求复合函数的导数。
\[\dfrac{\partial C}{\partial b_3}=\dfrac{dc}{dy}\dfrac{dy}{dz_3}\dfrac{\partial z_3}{\partial b_3}\]
注意到:
\[c=\frac{1}{2N}\sum|Y-y|^2=\frac{1}{2}(Y-y)^2\]
有:
\[\dfrac{dc}{dy}=\frac{1}{2}\times (-2)\times (Y-y) =0.84-1=-0.16\]
\[\frac{dy}{dz_3}=\frac{d(sigmoid(z_3))}{d(z_3)}=y(1-y)=0.84\times (1-0.84) = 0.13\]
而:
\[z_3 = h_1 \times w_5 + h_2 \times w_6 + b_3\]
求偏导数得:
\[\dfrac{\partial z_3}{\partial b_3}=1\]
综合得:
\[\dfrac{\partial C}{\partial b_3}=\dfrac{dc}{dy}\dfrac{dy}{dz_3}\dfrac{\partial z_3}{\partial b_3}=-0.16\times 0.13 \times 1 = -0.020\]
同理:我们可以计算出其他得偏导数。
举个例子:
\[ \begin{aligned} \dfrac{\partial C}{\partial w_1}&=\dfrac{dc}{dy}\dfrac{dy}{dz_3}\dfrac{\partial z_3}{\partial h_1}\dfrac{\partial h_1}{\partial z_1}\dfrac{\partial z_1}{\partial w_1}\\&=-0.16\times0.13\times0.50\times0.21\times1\\&=-0.002 \end{aligned} \]
而求完这九个偏导数,注意到我们只完成了一个数据点。
处理完四个点之后,我们需要给每个变量得偏导数求平均,再乘上步长,这就是一次迭代中这个变量应该改变的量,也可以让四个例子的结果更为准确。