想要了解一点点矩阵，我们需要从色彩的显示说起,也就是我们常见的RGB(Red Green Blue)色彩模式：

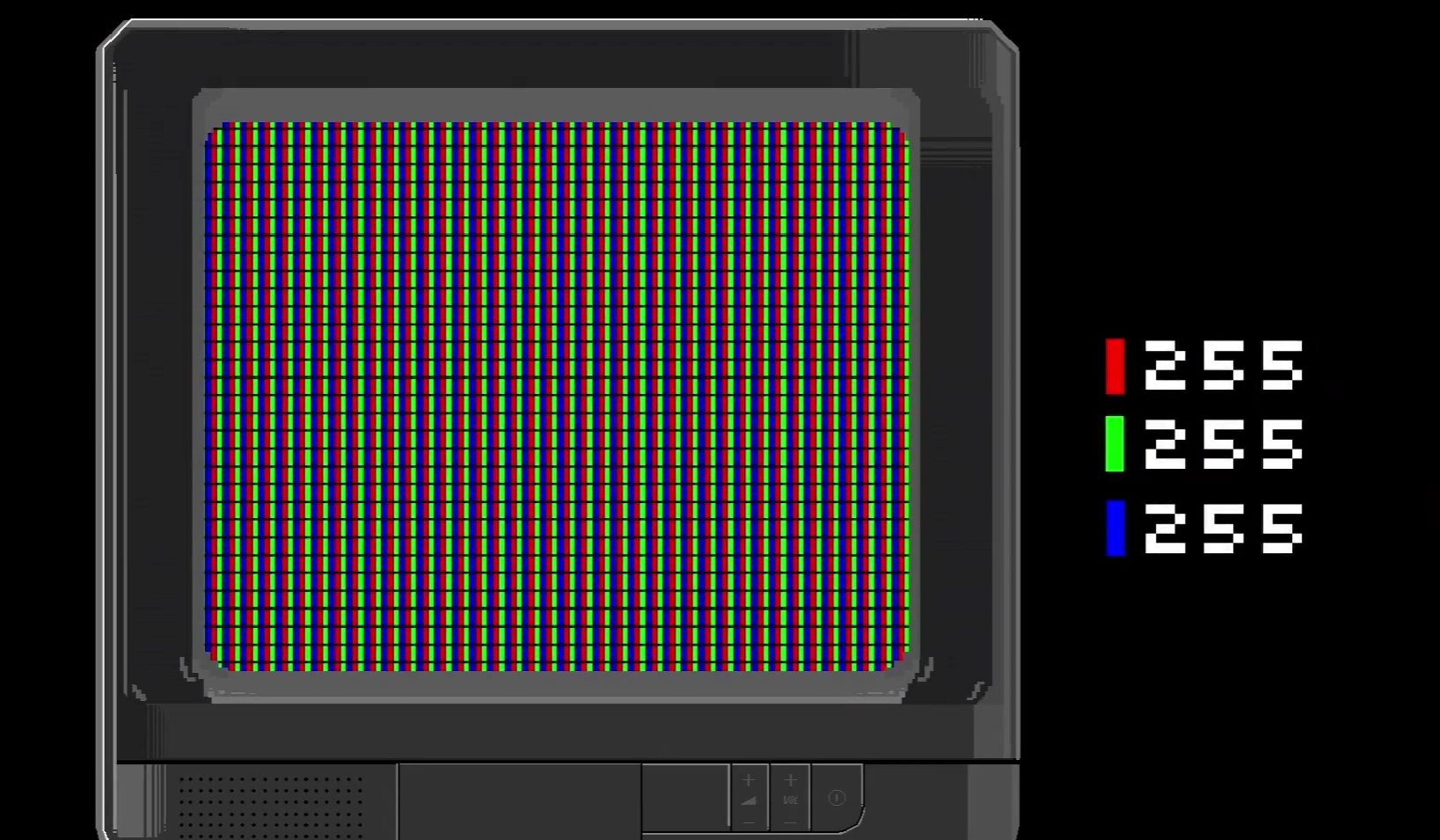
通过调整三种颜色的比例，我们可以得到不同的颜色

本文采用mathjax对数学公式进行渲染

这个调色器，其实就是一个矩阵(matrix)。

矩阵是操作向量的工具。想要理解矩阵，就要先理解向量(vector)

对于计算机来说，向量是一组有序的数；而对于中学数学老师来说，向量是一个有向线段。

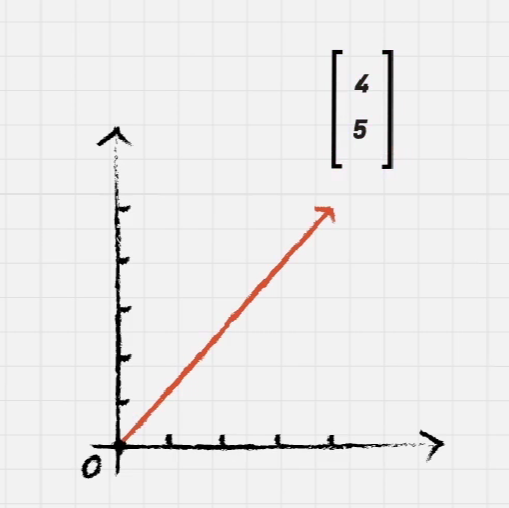
刚刚的RGB色值，也可以堪称一个向量：

可以表示为下列形式：

但如果我们定义一个坐标系，也可以在坐标系中把它标出来：

如果我们以R为x轴，G为y轴，B为z轴，建立空间直角坐标系：

它就在空间中的这个点

相应的，照片中每一个像素的色值，都可以在空间中找到对应的点。

接下来我们来认识一下矩阵：

先从一个我们小学二年级学过的二元一次方程组开始：

我们需要弄清楚Row和Column，即行和列的关系：

按照Row展开，它可以表现为如下的矩阵：

可以简化为Ax=b

注意它的系数是一一对应的！！！

容易看出，$x=1,y=2$是它的解

他也等价于下列图像：

而如果我们按Column展开，可以表现为如下的矩阵：

从列图像的角度去理解线性组合，也即 $Ax$ 就是对 $A$ 的列向量进行 $x$ 对应的组合（这种组合显然是线性的）。于是 求解 $Ax=b$ 也即对于给定 $b$ 是否能找到一种组合方式 $x$ 使得能够将 $A$ 的各列向量组合形成 $b$。

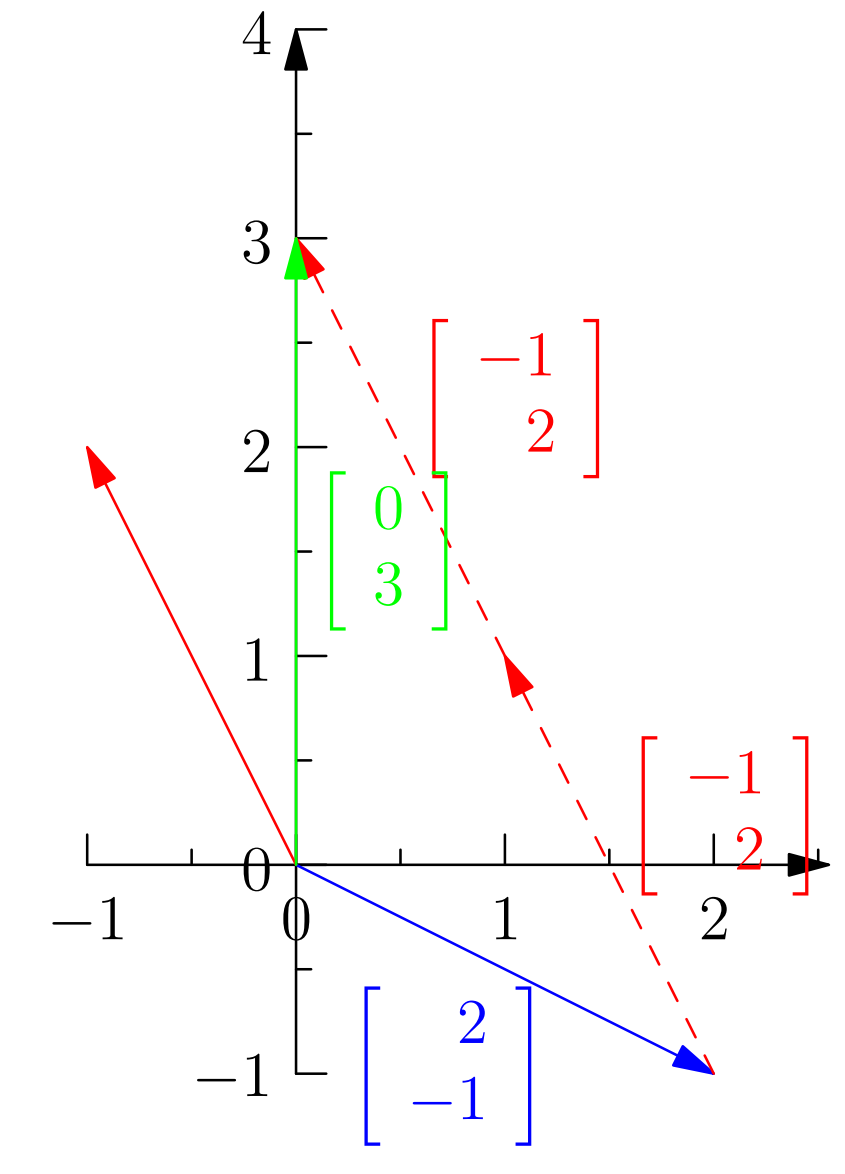
如果说原来x轴的基向量$\vec x=(1,0)$,则在上例中他的基向量变成了$\vec x’= (2,-1)$ ,同理, $\vec y’=(-1,2)$,我们需要寻找对应的x，y对两个基向量进行线性组合，让它的结果为向量(0,3)

也可以看成是在一个新的坐标系中，以x’和y’为基向量，寻找对应的x,y得到目标向量(0,3)

此时，我们就变换了坐标系。

回到我们熟悉的神经网络方程组(不熟悉的话马上就熟悉了)：

不看阈值b,可以将他写成下列的矩阵形式：

即$Z=WX$

同样的道理，新的坐标系的基向量就变成了(W1,W3)和(W2,W4)。这就是矩阵的作用，通过改变基向量来改变坐标系。

同时，矩阵还能将二维平面的点映射到三维空间中去。比如下面的例子：

可以在三维坐标系中这么表示：

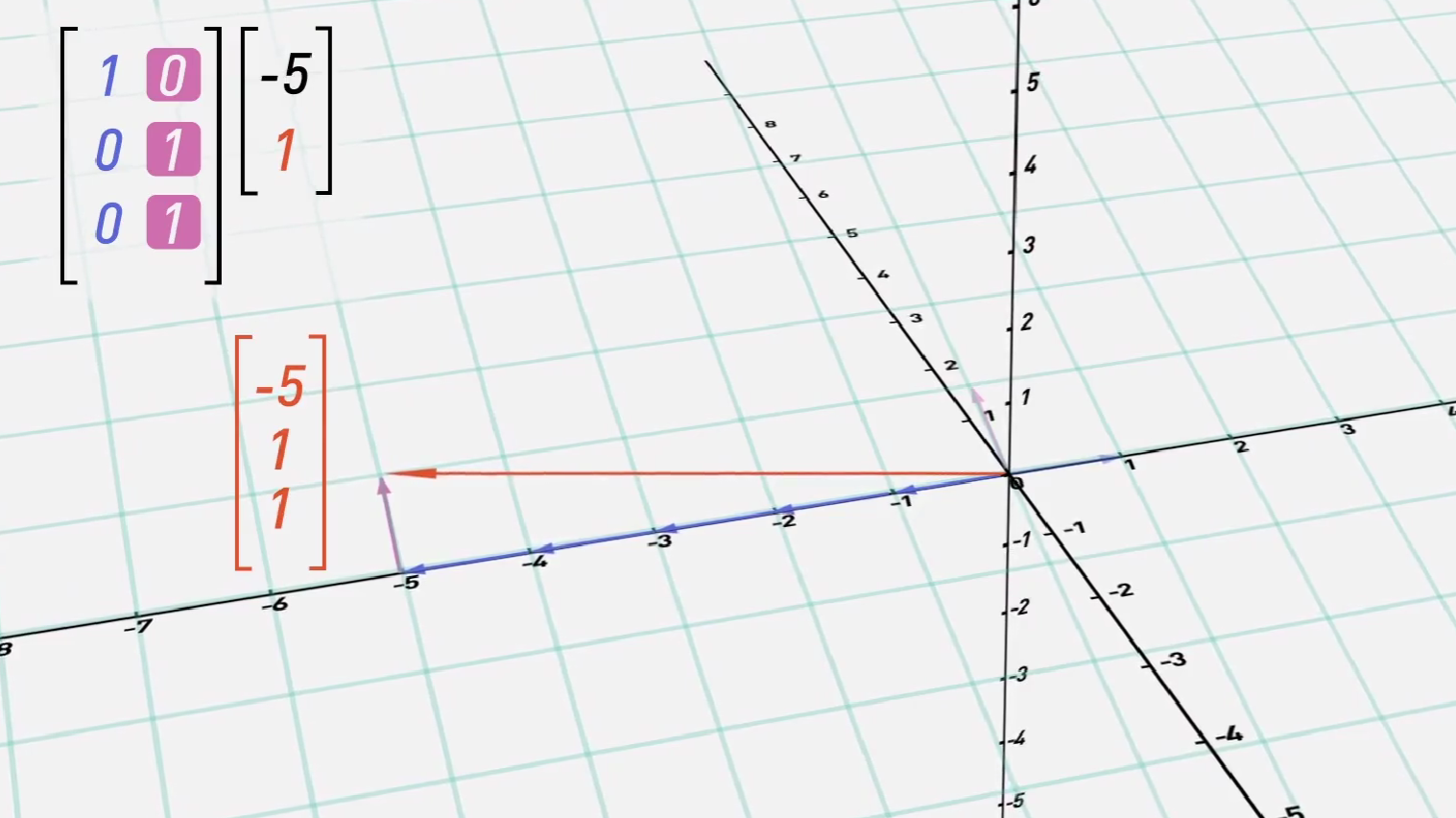
所以再回到开始的那个问题：我们可以为RGB图案加上一个色彩矩阵，如这个例子中，可以让R’与B’都为0，为图片加上绿色的滤镜。

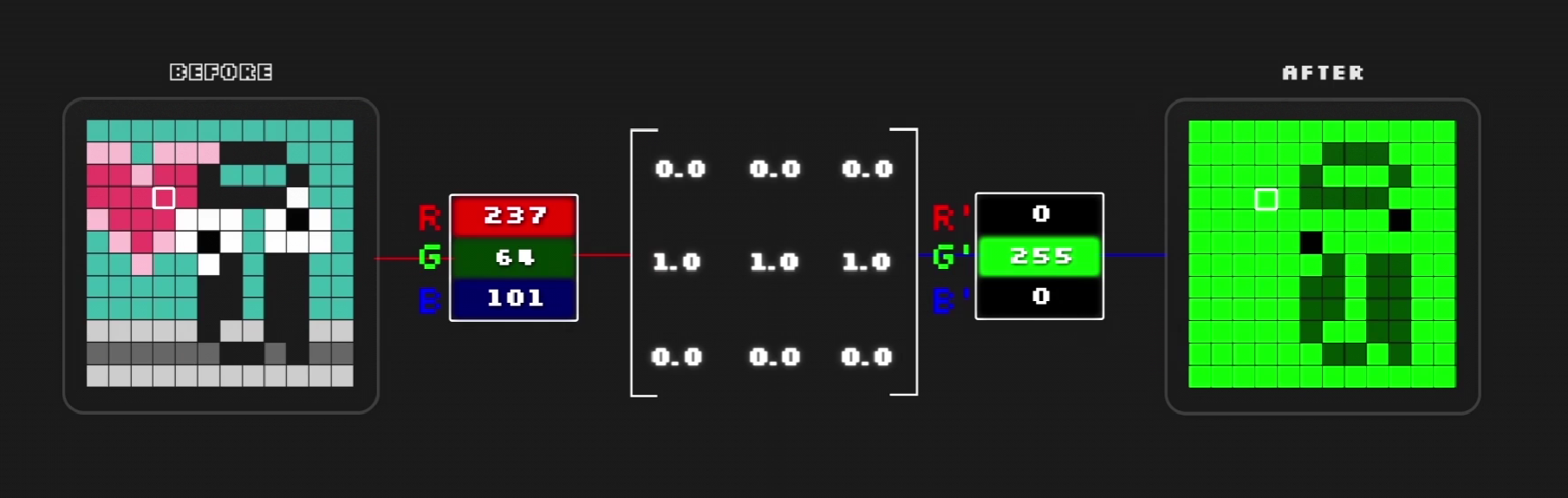
对于神经网络来说，写成矩阵、向量相乘的原因主要是快。回想开头784维向量的例子：由于计算机的并行优化，可以同时对多个输入数据进行处理，我们可以非常快速的完成784维向量的计算。

这就是简单的矩阵，它其实没那么可怕。