先考虑一个问题：如何用一条线把(0,0),(0,1),(1,0),(1,1)这四个点分成两类？

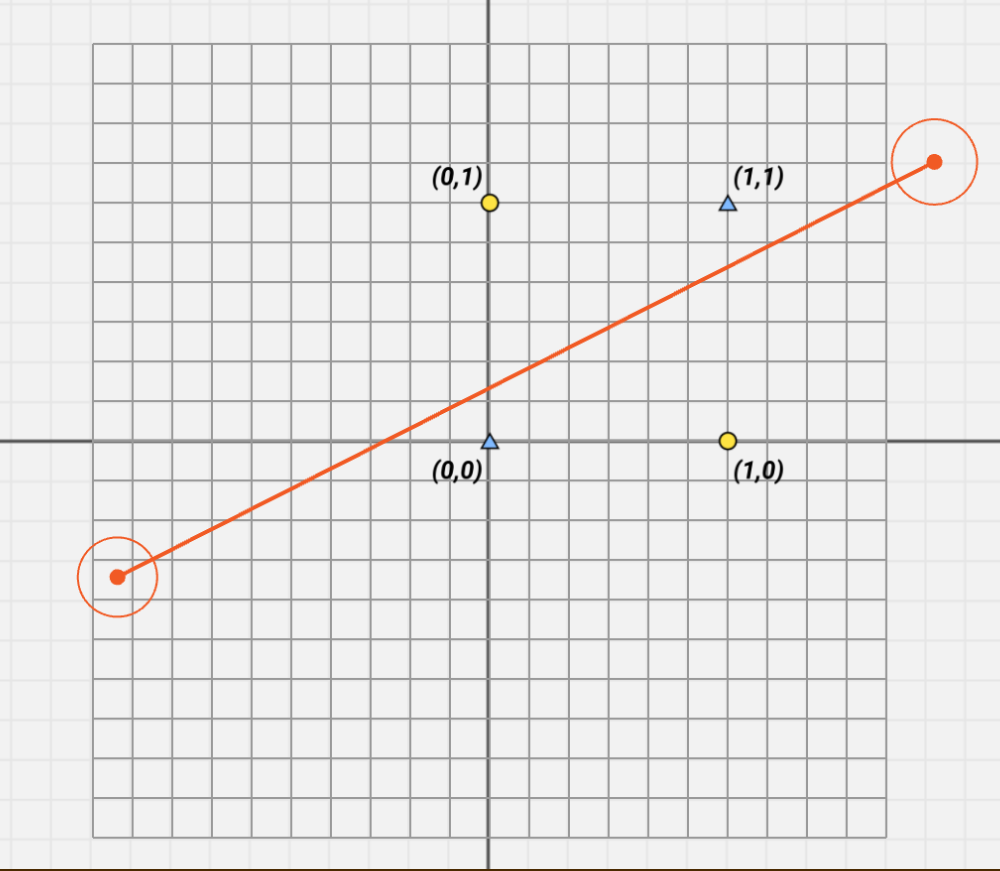
单纯的改变线肯定是不行的，我们要使点小花招：改变空间

机器学习的序幕已经被拉开

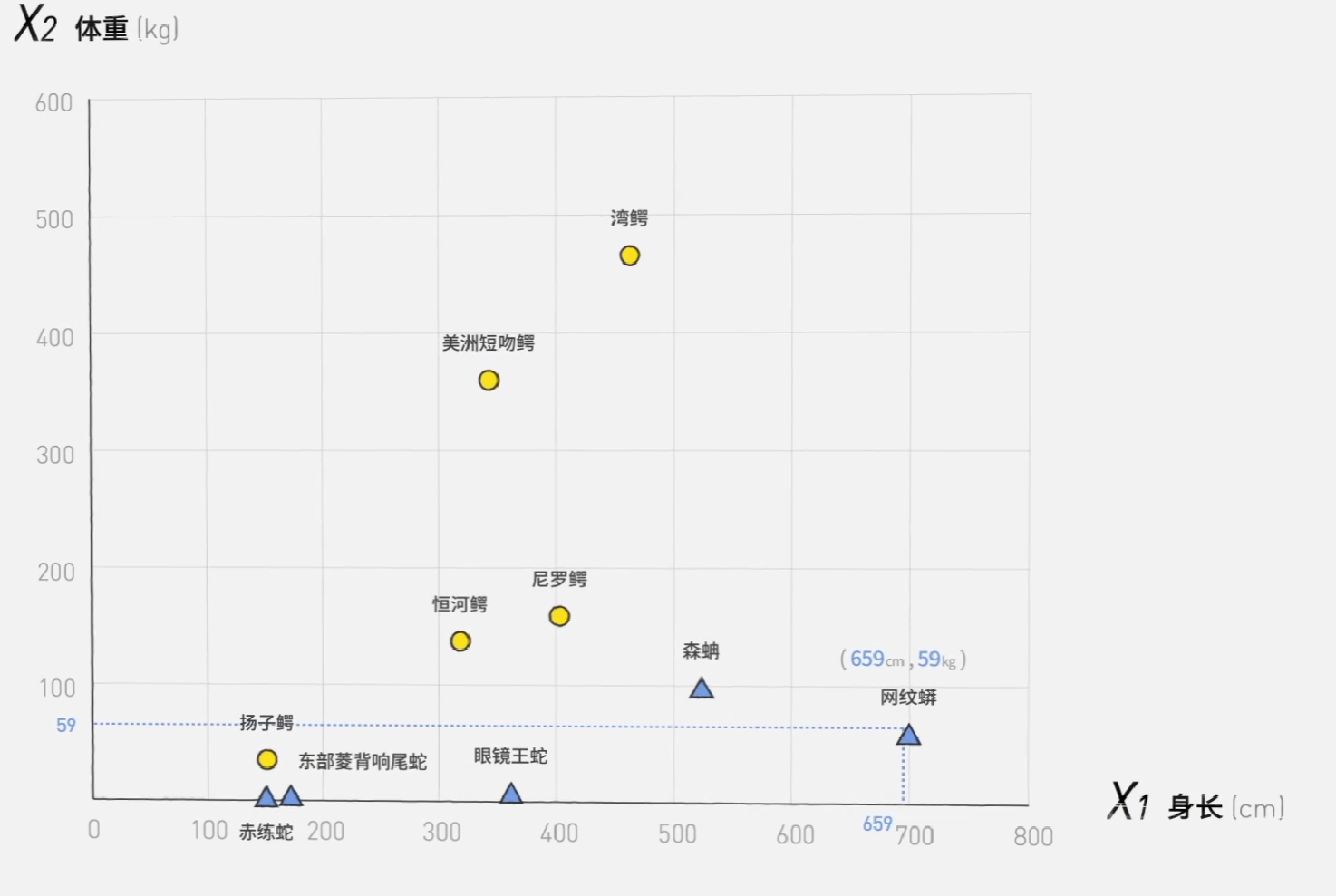
前面所讲过的二元分类器，有一个缺点：它太直了，处理不了数据有交叉的情况。

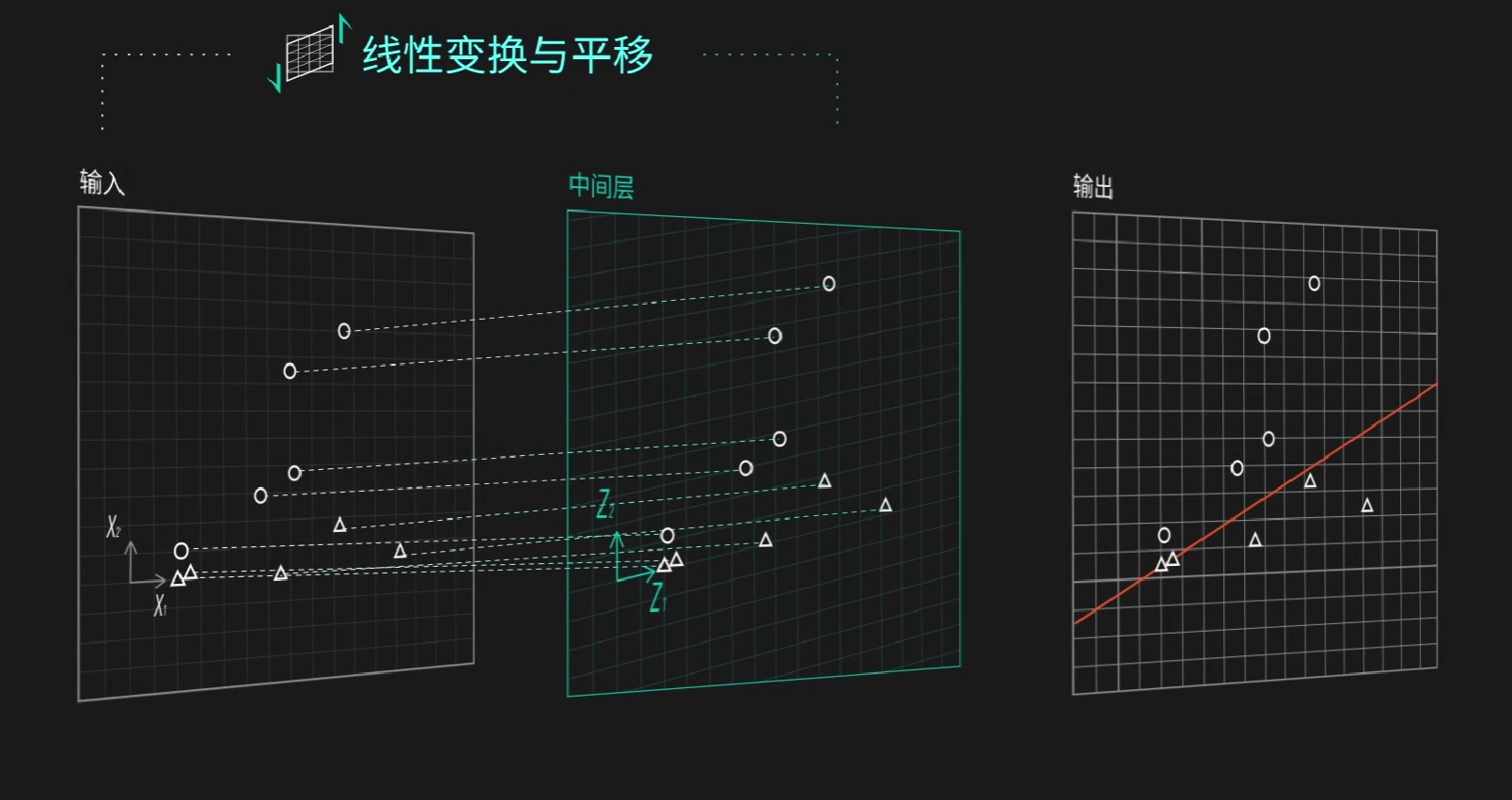
直到人们意识到，我们可以弯曲整个坐标系：

我们加入一层中间层，它的作用就是改变坐标系

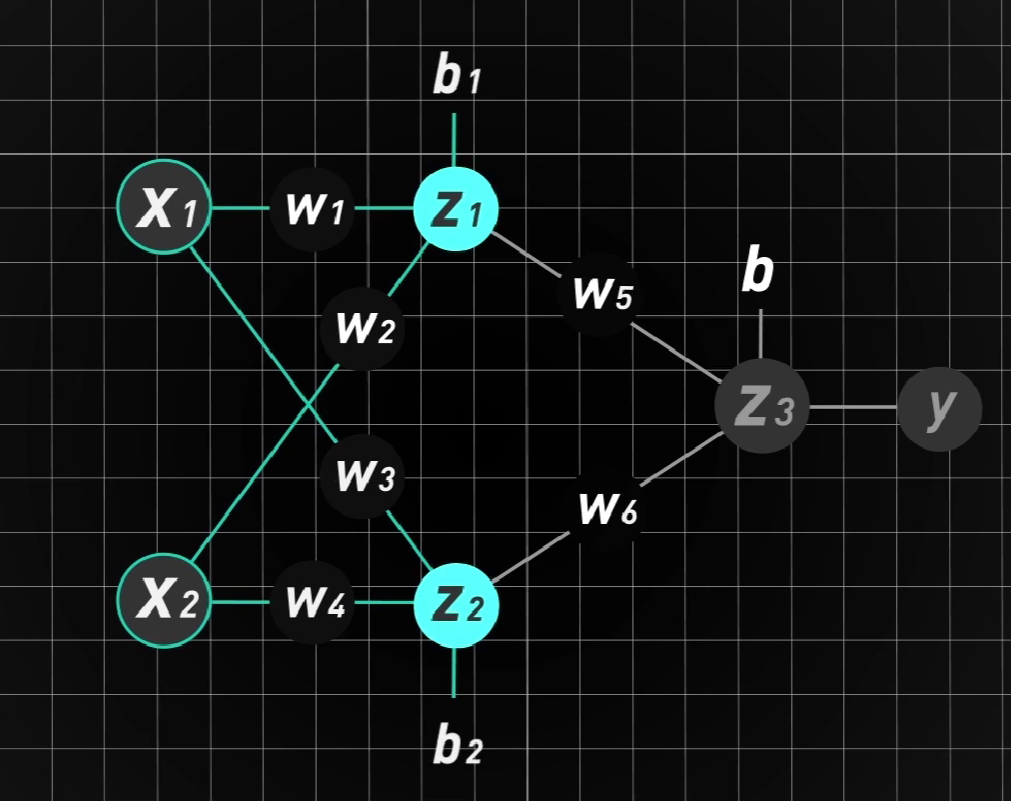
在这个新结构中，容易发现： \[Z_1=W_1\times X_1 +W_2 \times X_2 + b_1\] \[Z_2=W_3\times X_1 +W_4 \times X_2 + b_2\]

不看阈值b,可以将他写成下列的矩阵形式： \[\left[ \begin{matrix} W_1&W_2 \\ W_3&W_4 \end{matrix} \right ]\left[ \begin{matrix} X_1\\ X_2\end{matrix} \right ]=\left[ \begin{matrix} Z_1\\ Z_2\end{matrix} \right ]\] 即\(Z=Wx\)

但是，无论我们怎么改变W矩阵，还是无法将这四个点分开，因为它始终属于线性变换！

解决方案很简单：再加一层非线性变换！

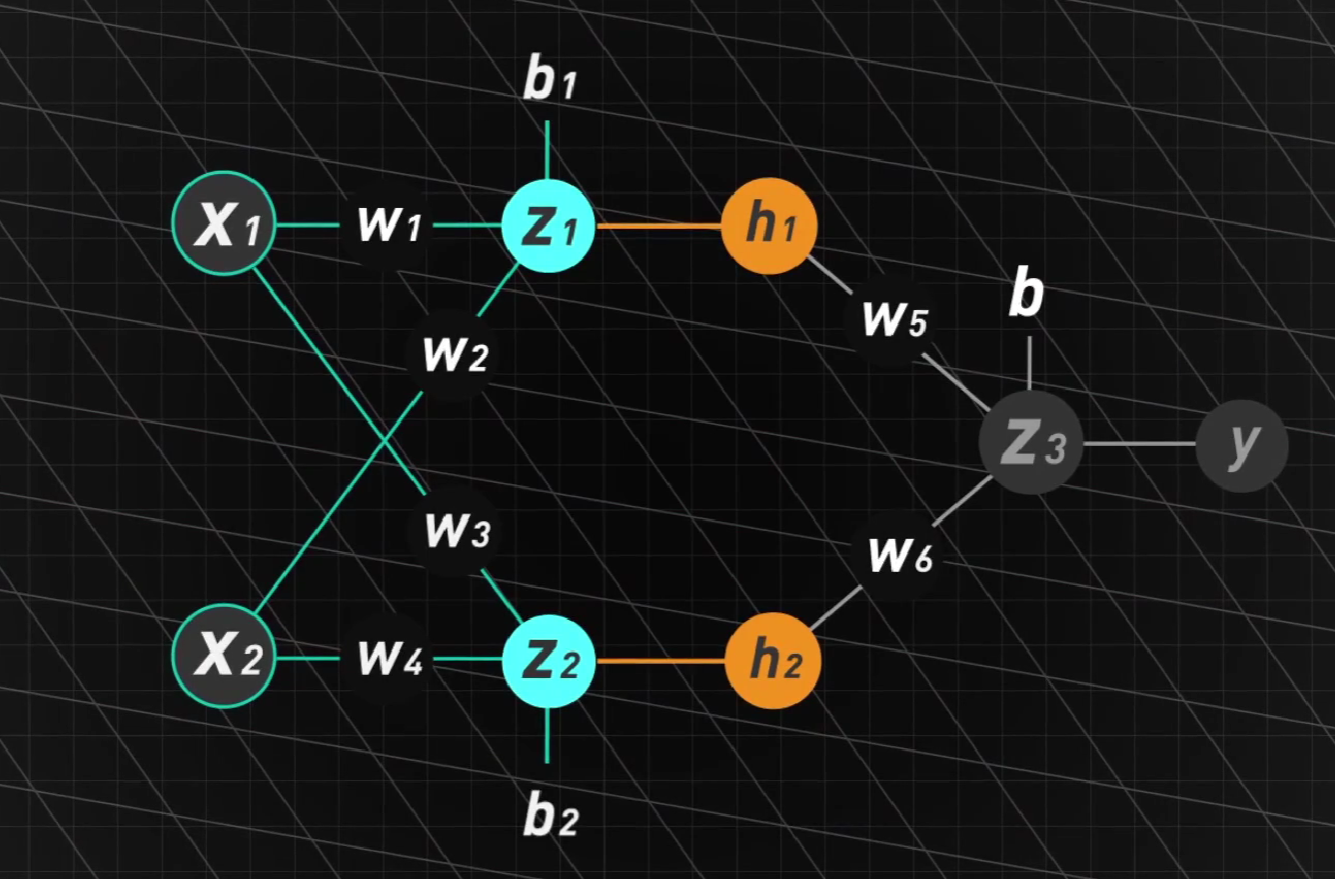
隆重介绍：激活函数(Activation Functions)

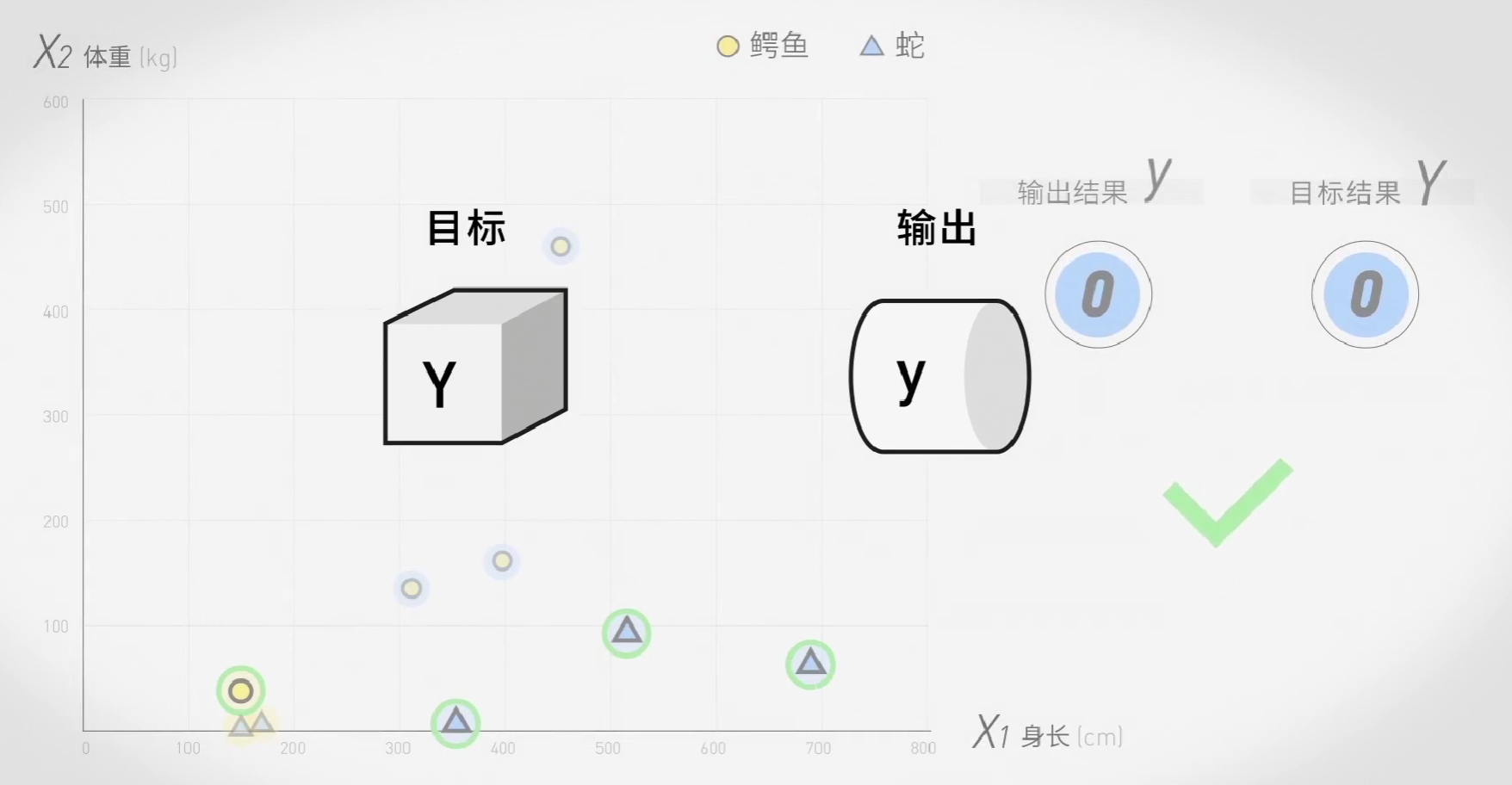
它是以一种特定的规则，让输入数据以一种特定的方式进行输出。比如阶跃函数(step function)，在关于鳄鱼和蛇的问题中，输出0或1其实就是阶跃函数运作的结果。

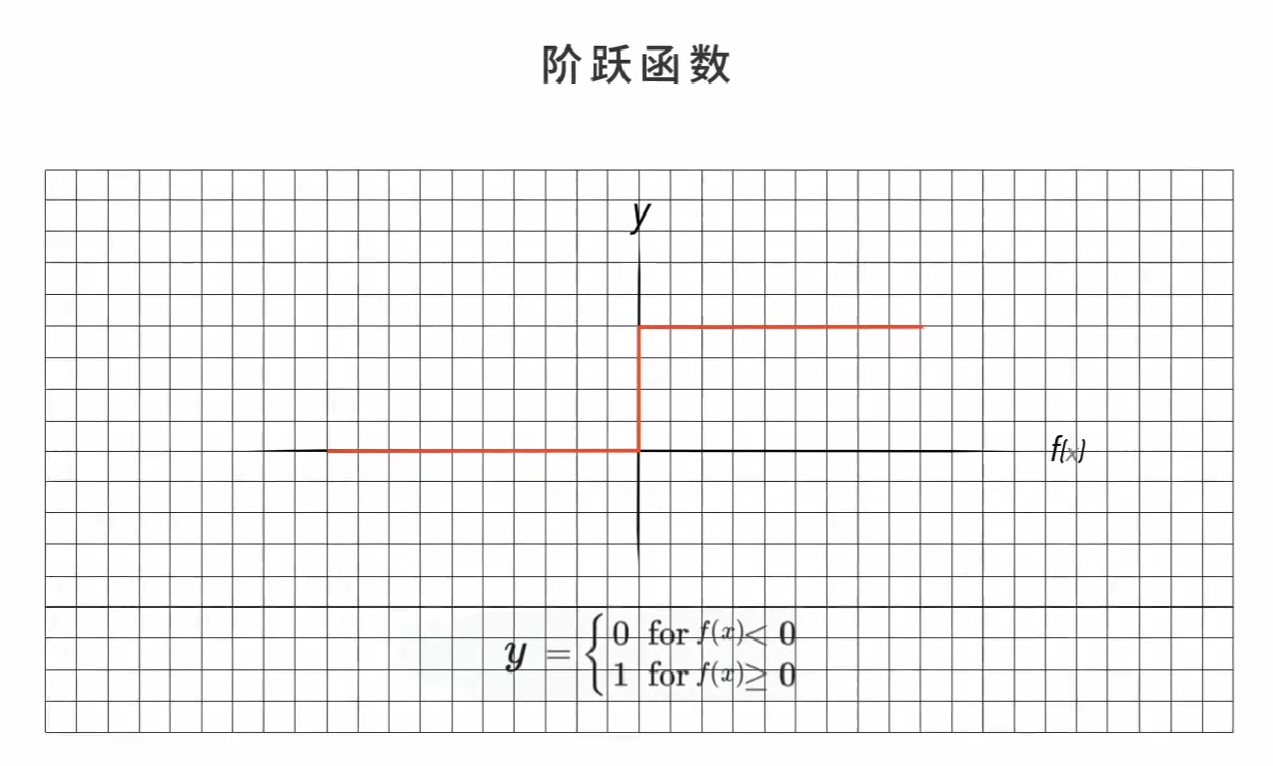
除此以外，在机器学习中还有三种常见的激活函数：

逻辑函数(sigmoid function)：\(\sigma(x)=\frac{1}{1+e^{-x}}\)

线性整流函数(ReLU function)：\(h(x)=\begin{cases} 0&x<0 \\ x & x\geq0 \end{cases}\)

双曲正切函数(tanh function):\(tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\)

让我们回到开始的问题：现在，我们可以再加一层：

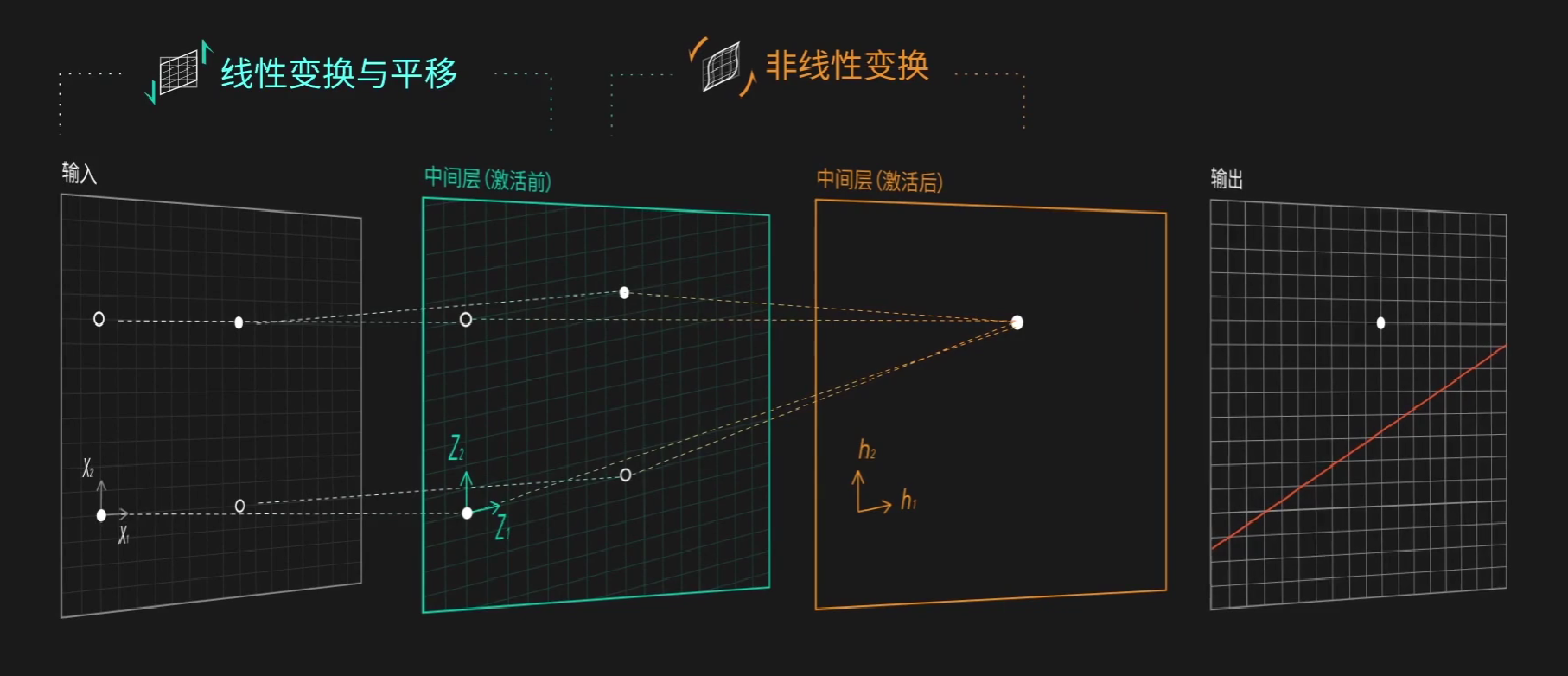
首先我们可以通过线性变换对原来的四个点进行平移：

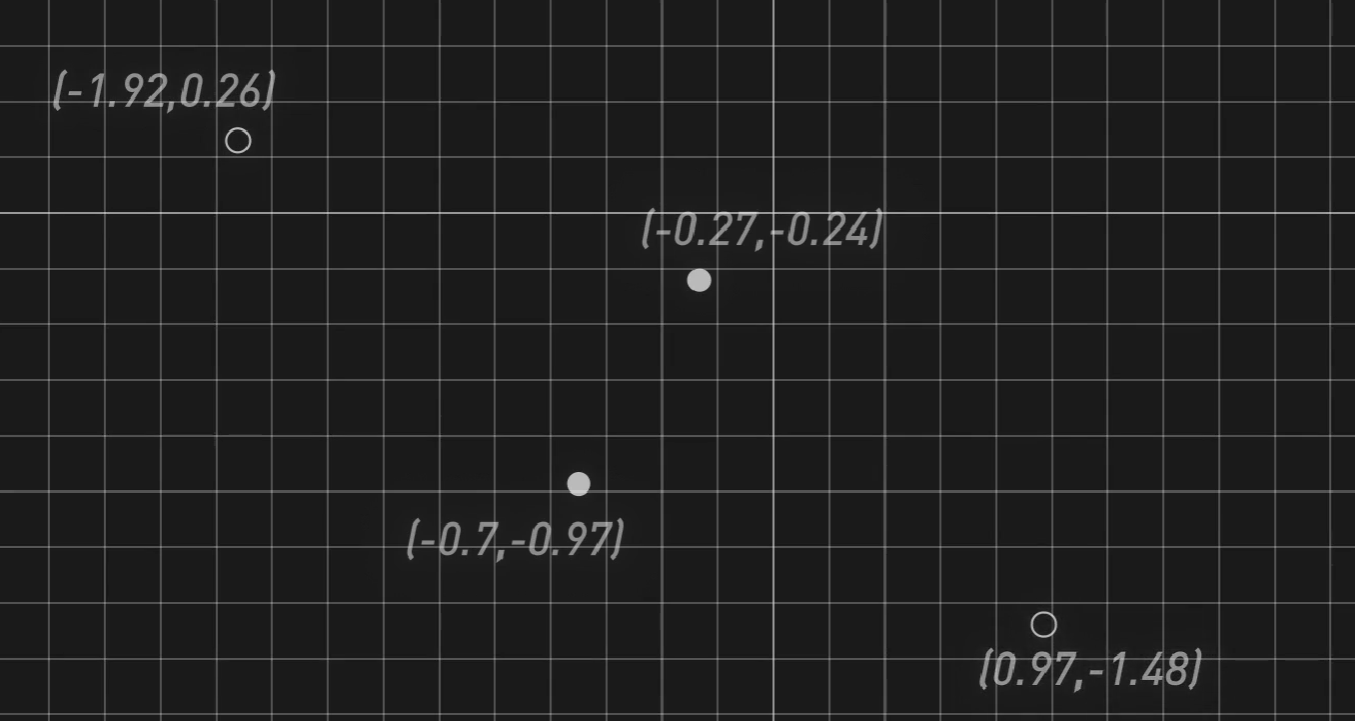
再通过阶跃函数，让原本在第三象限的两个点变为(0,0),另外两个变为(0,1)和(1,0)，这样我们就能很自然的将两类点分开。

由此，我们便搞定了分类异或问题。

但是如果我们试图在二维平面内分类一个圆环呢？

这个问题就有点难，但是我们可以试图对问题进行升维处理,把二维平面变成三维空间:

再使用二维平面进行分割，我们就能得到不错的区分度：

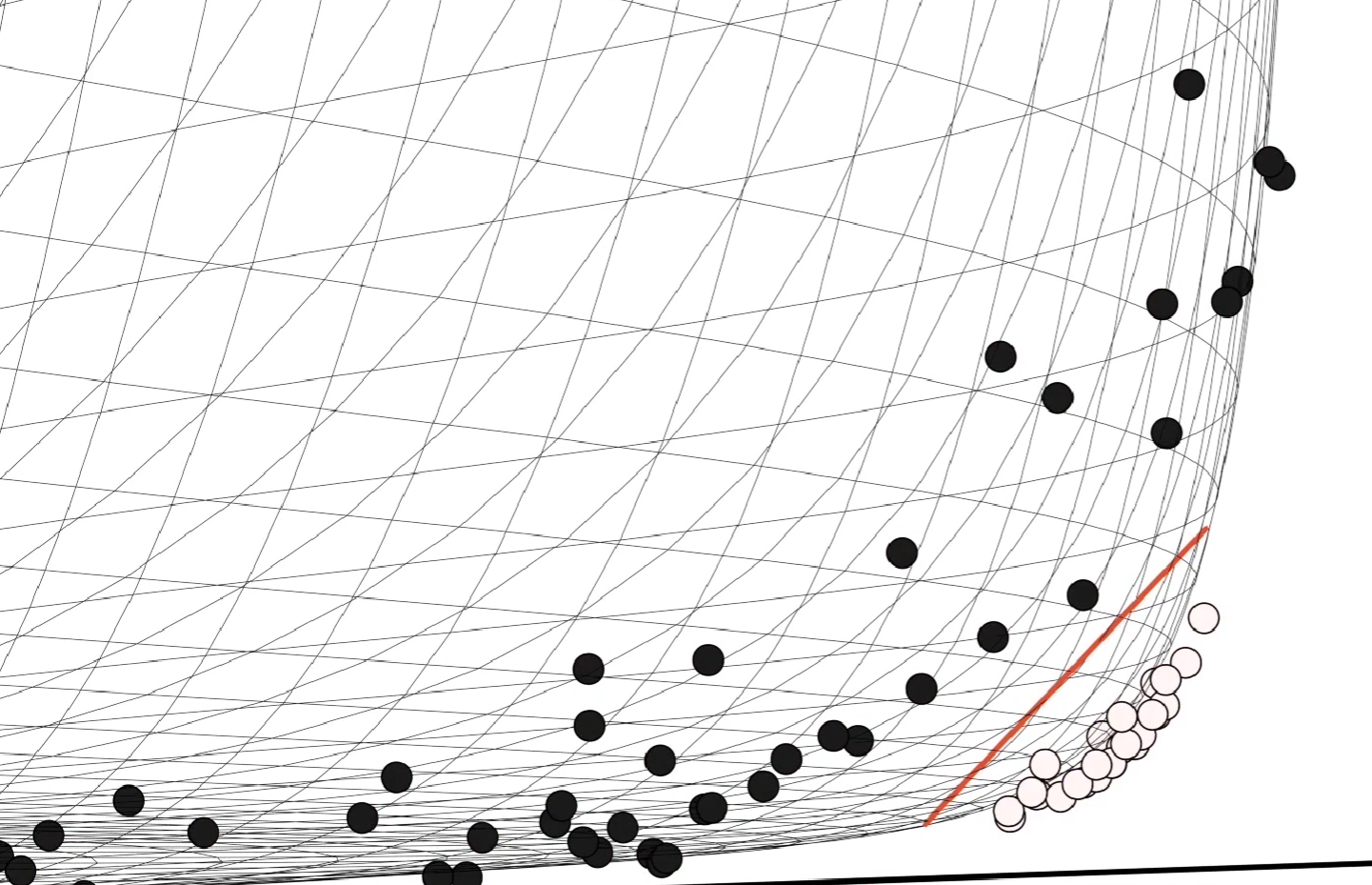
所谓升维，就是将低维的密集数据在高维空间中变得稀疏，从而更好的分开。

将三维空间的分割面再次投影二维平面，就是一个圆。

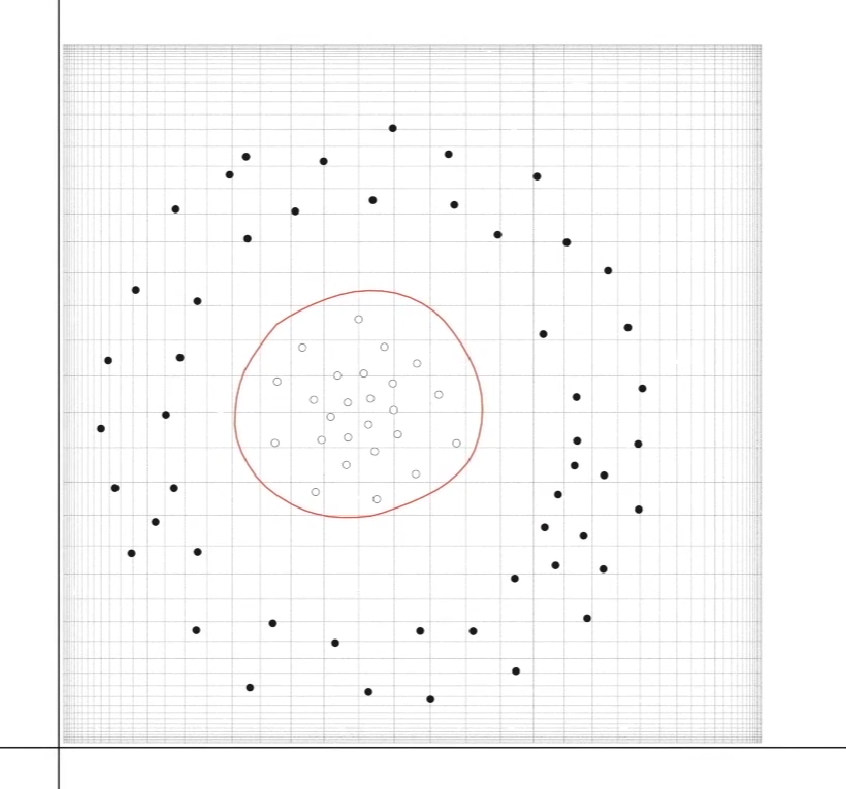
原本扭曲的异或分类还原之后，坐标系会变直，分割线会变弯。但我们都知道，他的本质还是一条直线。