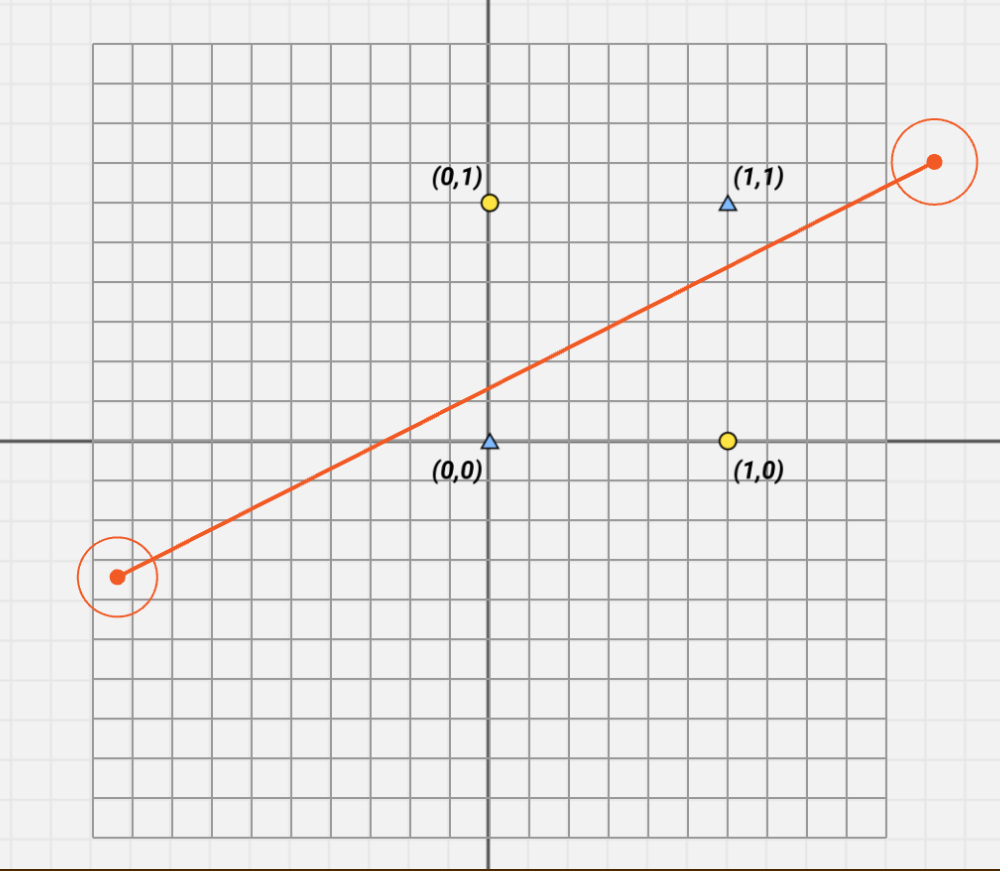
用横坐标代表身长，纵坐标代表体重，在坐标系中标出鳄鱼和蛇。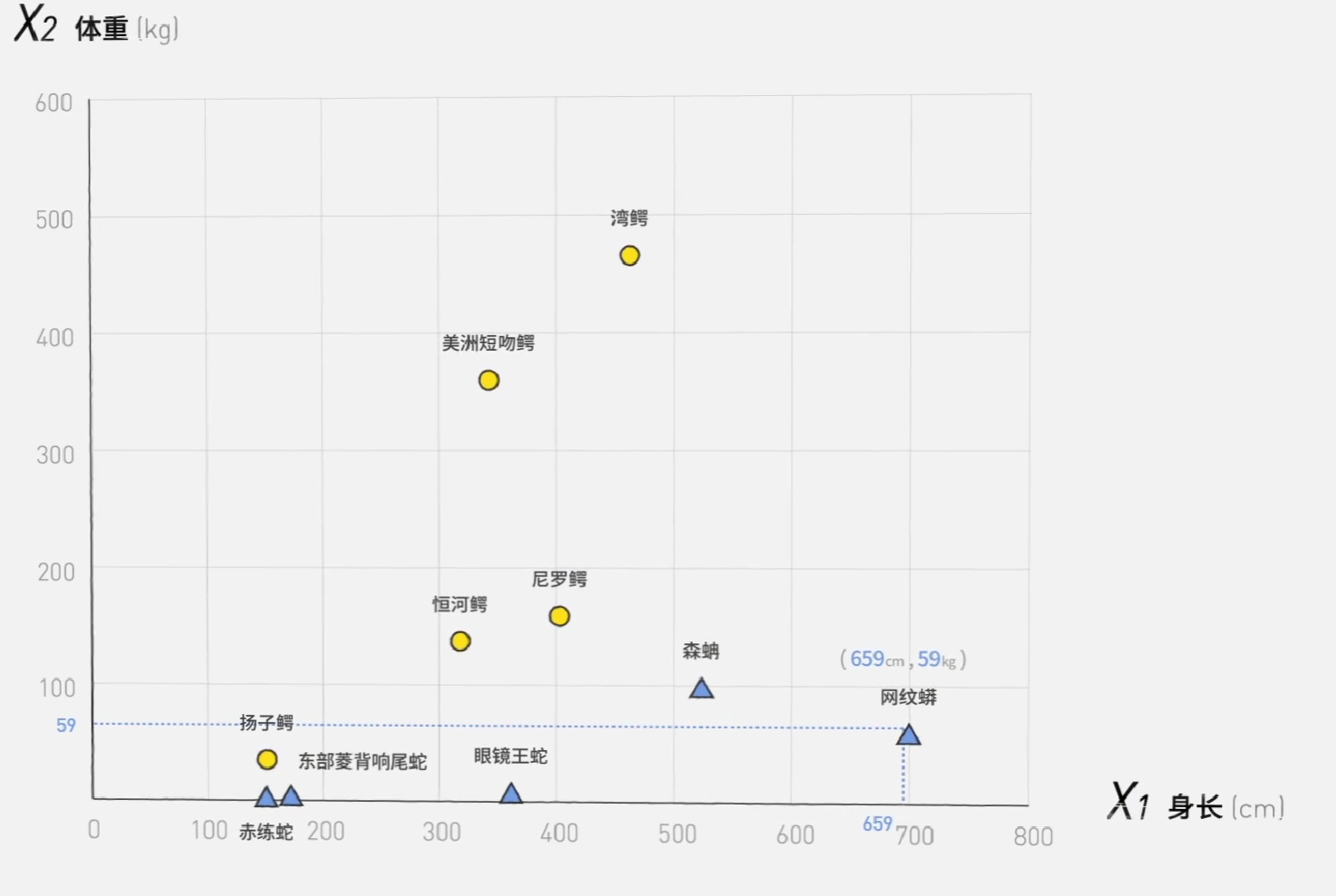 鳄鱼和蛇 我们要做的，就是画一条线把他们两个分开。 非常的简单，对不对？

很容易知道，W改变的是斜率，而b改变的是位置。

这个问题的本质是分类，而分类就是智能的源头。

神经元，阈值，权重，正好跟生物知识一一对应。我们也可以把他抽象成数学知识。

如果\(f(x)>b\),即输入信号大于阈值，输出为1，反之为0。

之后涉及到的所有复杂神经网络，都是由这样的神经元所组成的。我们只要让它开始学习就好了。

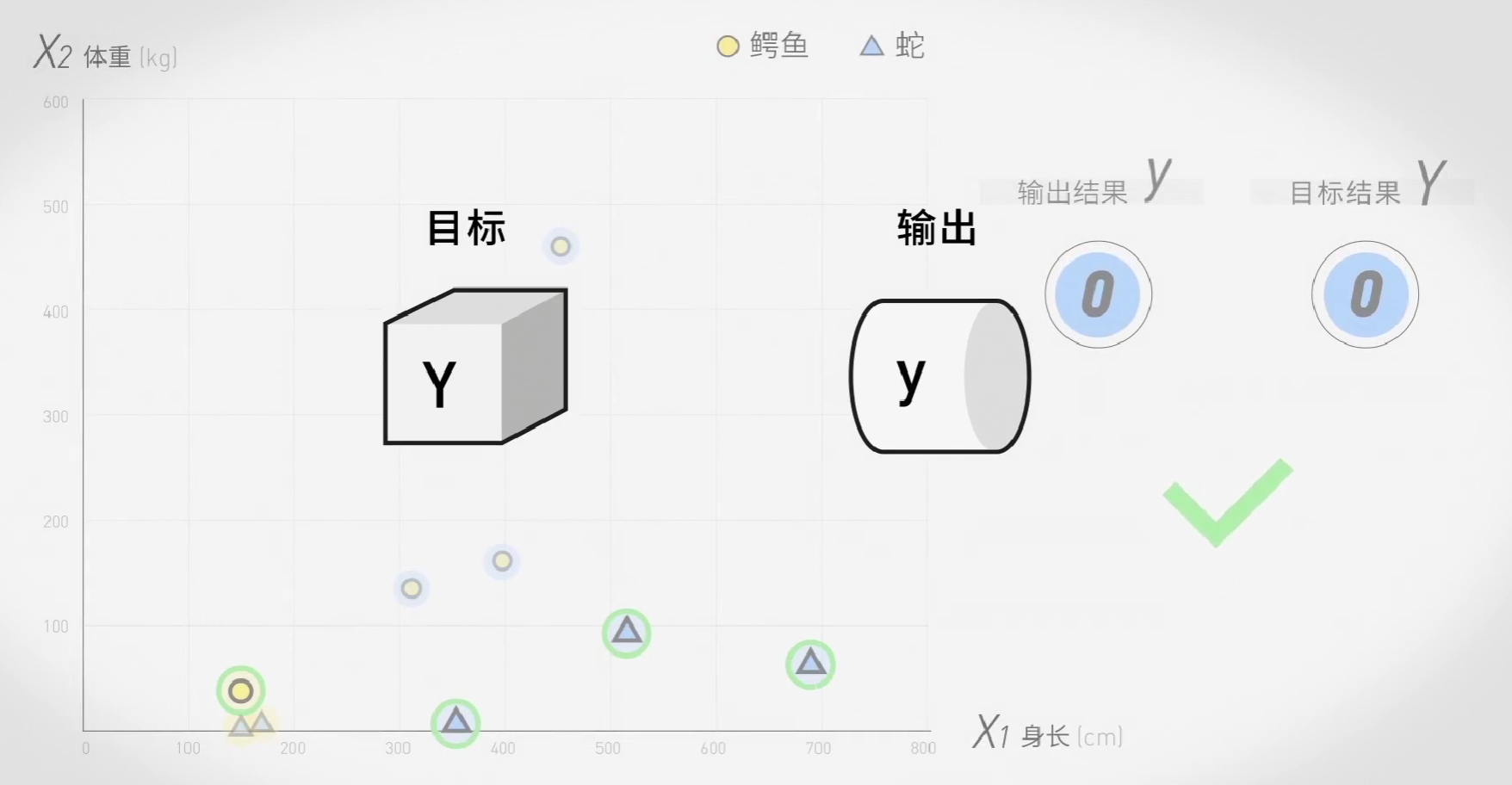
流程很简单：输入，识别，输出，判断

让我们回到鳄鱼和蛇的问题：输入特征就是输入动物的身长和体重，识别特征就是将数据乘以对应的权重并相加，输出结果就是将f(x)与阈值b进行比较，大于阈值输出1，小于阈值输出0，再与已知的数据进行比较，判断对错：而判断对错，正是机器学习的核心环节。

现在，我们把输出结果命名为y，目标值为Y，只有y和Y都是0或者1，结果才正确，不一样就是错误。

而机器学习，就是通过不断调整权重W和阈值b，来让结果尽可能的正确。

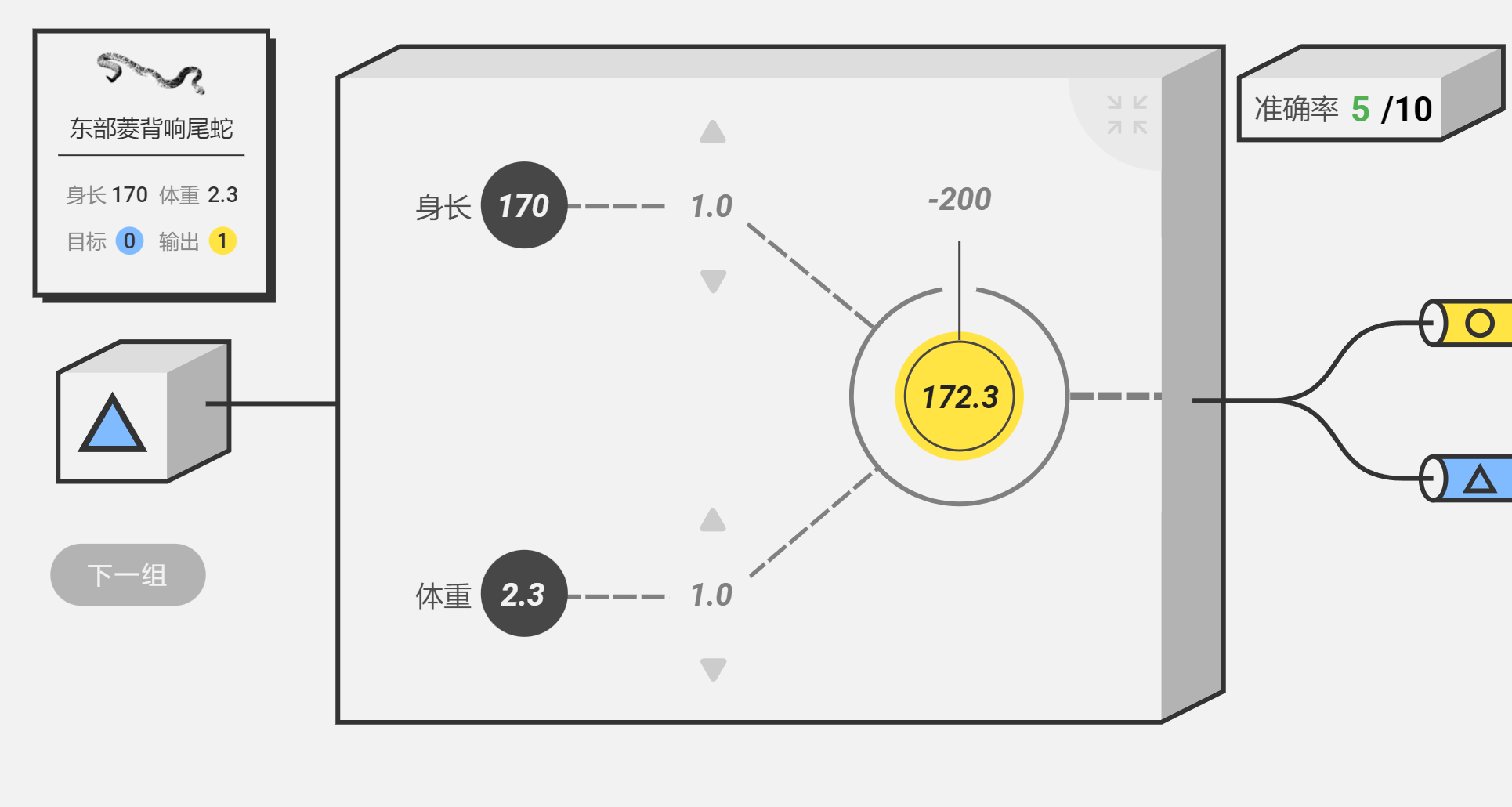
用数学语言描述刚刚的过程，可概括为如下公式：

\[W_{i(t+1)}=W_{i(t)}+\Delta W_i\]

很容易想到，让机器自动调整的关键就是让机器知道\(W_i\)是大了还是小了。而Y是真实值，y是输出值，如果Y与y一样，则\(Y-y=0\)，使得\(\Delta W_i = 0\)，\(W_i\)不调整;如果\(Y-y=1\)，则真实值比输出值偏大，要提高\(W_i\)让\(f(x)>b\)才能达成目的，反之亦然。同时，还需要乘以\(X_i\)，这个点的X越大，对整个函数的影响也要越明显，所以我们列出以下式子：

(r是机器的学习率，可参见梯度下降的有关知识) \[\Delta W_i = (Y-y)\times X_i \times r\] \[W_{i(t+1)}=W_{i(t)}+(Y-y)\times X_i \times r\] 同时，b也要进行相应调整： \[\Delta b = (Y-y)\times 1 \times r\]

早在1957年，Frank Rosenblatt就发明了这种感知器，但他存在一个致命的缺陷：很多数据无法用一条直线，一个平面甚至一个超平面分开，而这就涉及到变换坐标系的有关知识，而它与线性代数 | Linear Algebra又紧密相联。