人工智能导论上机实验及课程论文
结课论文采用Latex进行撰写,可以直接在Github仓库查看PDF版本的论文(https://github.com/dekrt/Reports)
十五数码问题求解算法及性能比较
Fifteen Digital Seeking solutions and comparison
 |  |
| 图 1-1 八数码问题 | 图 1-2 十五数码问题 |
1 | //定义二维数组来存储数据表示某一个特定状态 |
- 曼哈顿距离(Manhattan Distance):对于每个方块,计算其在网格上从当前位置到目标位置的最少移动次数(只考虑水平和垂直移动)。所有方块的曼哈顿距离之和就是启发式的估计值。计算公式为 $ h(n) = |n_x - goal_x| + |n_y - goal_y| )$,其中 $( n_x, n_y )$ 是当前节点的坐标,$( goal_x, goal_y )$ 是目标节点的坐标。

线性冲突(Linear Conflict):这是对曼哈顿距离的一种改进。如果两个方块在同一行或列中,并且都处于彼此的目标路径上,那么它们之间存在线性冲突。对于每对发生冲突的方块,需要额外的移动次数来解决这个冲突。因此,总的启发式估计值是曼哈顿距离加上所有线性冲突的调整值。
模式数据库(Pattern Database):这是一种预先计算并存储特定模式或方块组合的最优解的方法。对于十五数码问题,可以创建几个模式数据库,每个数据库对应网格上一组特定的方块。然后,将这些数据库中的值相加以得到启发式估计。
这些启发式函数在实践中的表现取决于具体的问题实例和算法的实现细节。通常,更复杂的启发式函数(如线性冲突和模式数据库)可以提供更准确的估计,但同时也可能需要更多的计算资源。在本次实验中,选择的启发函数为:汉明距离(Hamming Distance)、曼哈顿距离(Manhattan Distance)和线性冲突(Linear Conflict)。
状态转换和扩展:在每一步中,算法探索所有可能的移动(上、下、左、右),生成新的状态。每个新状态都会根据其成本(已走步数+启发式估计成本)加入到优先队列中。
初始状态和目标状态:在本实验中,初始状态从可以通过Console控制台进行输入,可以针对不同难度的测试样式进行测试;目标状态是数字顺序排列(1到15)和一个空格(0),在代码中已经做好定义。
实验设计
实验目标和评价指标
本实验的主要目标是研究并比较不同求解方法在解决15数码问题时的性能。为了实现这一目标,需要定义具体的评价指标,这些指标将用于量化和比较各种算法的有效性。主要评价指标包括:
- 求解时间:从算法开始到找到最终解的总耗时。这是衡量算法效率的主要指标之一。
- 中间状态数:在达到最终解决方案的过程中,算法生成并考察的总状态数量。中间状态数反映了算法的空间复杂度,即算法在寻找解决方案的过程中所需处理和存储的信息量。
- 步数:从初始状态到达目标状态所需的最小移动次数。这反映了算法找到解决方案的优化程度。
设计不同难度级别的15数码问题实例
低难度实例
在低难度实例中,初始状态通过对目标状态进行5到10步随机合法移动得到。这些移动较少,因此解决起来相对容易。如图3-1、图3-2所示:
- 初始状态:5 1 3 4 2 0 7 8 10 6 11 12 9 13 14 15
- 目标状态:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0
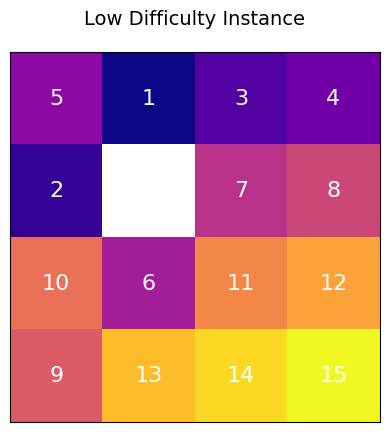 |  |
| 图 3-1 低难度十五数码实例 | 图 3-2 目标状态 |
其最短步骤如下所示:
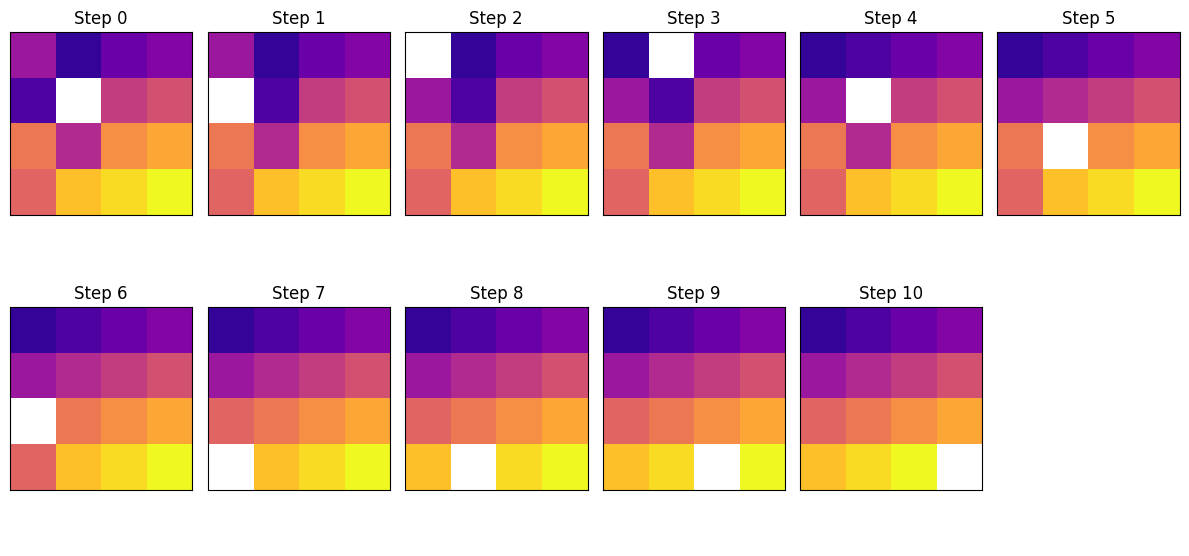
高难度实例
高难度实例通过对目标状态执行41步的随机合法移动来生成。这个实例更难解决,需要更多时间和资源。
- 初始状态:11 9 4 15 1 3 0 12 7 5 8 6 13 2 10 14
- 目标状态:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0
 |  |
| 图 3-4 高难度十五数码实例 | 图 3-5 目标状态 |
其最短步骤如下所示:
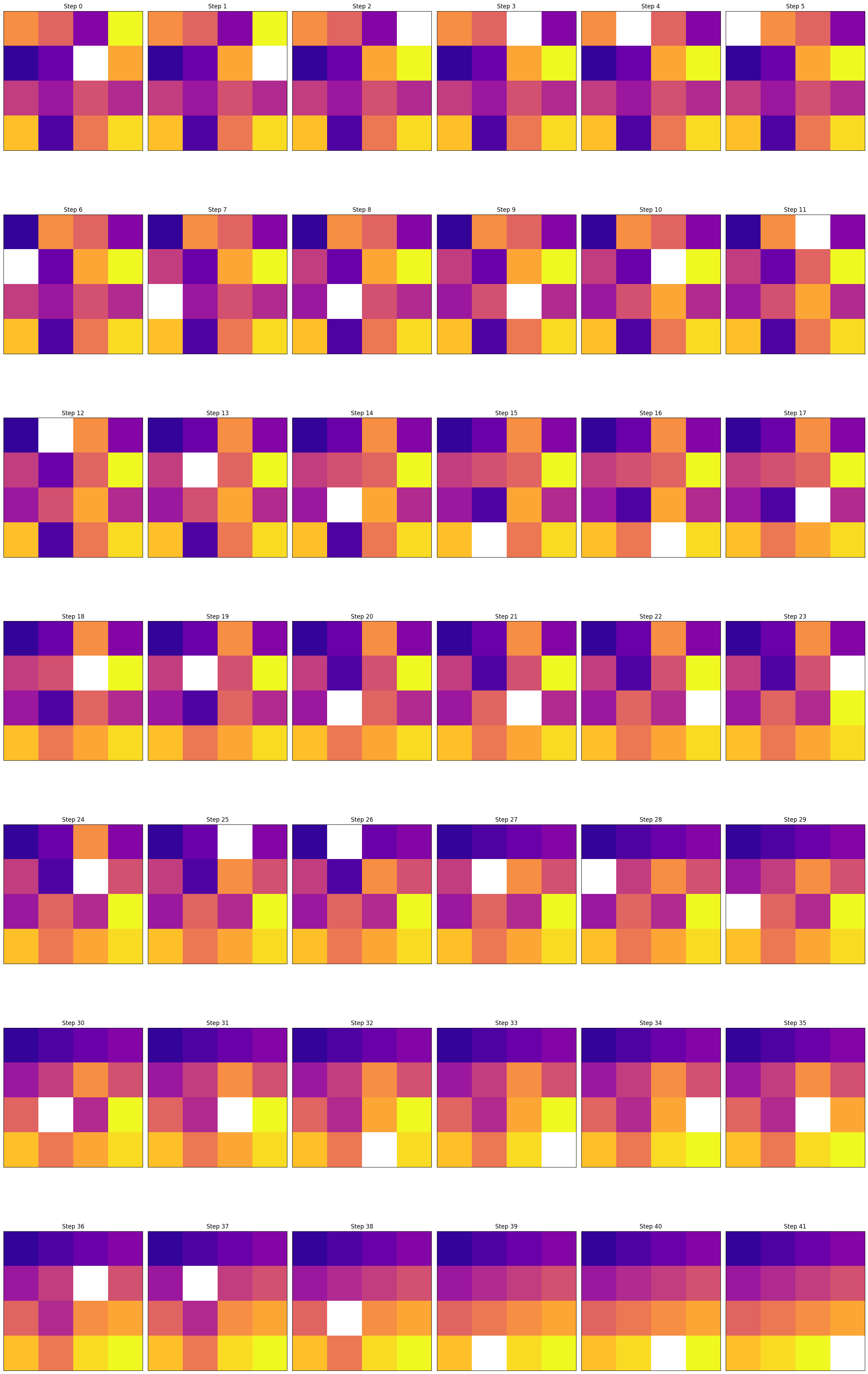
在设计实验时,可以使用这些具体实例来评估不同算法在解决15数码问题上的性能。通过对这些不同难度级别的实例进行测试,可以更准确地衡量和比较各种求解方法的时间和空间效率。
选择并实现不同的搜索算法
不同的启发函数
在本实验中,我们将专注于使用A*搜索算法,并采用三种不同的启发式函数来评估算法的效率和有效性。以下是我们将实现和比较的三种启发式函数:
- 汉明距离(Hamming Distance):这种方法计算当前状态中与目标状态不匹配的方块数量。对于15数码问题,就是计算除空格外,放置位置错误的方块数量。汉明距离简单易计算,但可能不够精确,因为它没有考虑到达目标状态所需的实际步数。
- 曼哈顿距离(Manhattan Distance):此方法计算每个数字方块从其当前位置到目标位置的格子数总和。对于每个方块,其曼哈顿距离是其在行和列上的距离之和。曼哈顿距离考虑了方块需要移动的实际距离,因此比汉明距离提供了更精确的启发式估计。
- 线性冲突(Linear Conflict):这种方法在曼哈顿距离的基础上增加了额外的考虑因素。如果两个方块在达到其最终位置之前需要交换位置,那么这被认为是一个线性冲突。例如,如果两个方块在同一行或同一列中并且它们的目标位置也在这一行或列中,但它们的顺序是错误的,那么每对线性冲突将增加两步到总曼哈顿距离中。这使得启发式估计更加接近实际的最小步数。
在本次实验中,我们通过定义宏变量的方式来选择不同的启发函数,在程序编译的过程中会自动选择我们需要的启发函数,如下述代码所示:
1 | // 通过宏定义确定启发函数 |
实验方法
对于每种启发式函数,将使用A*搜索算法求解一系列不同难度级别的15数码问题实例。实验将记录每种情况下的求解时间和步数,以及算法的空间复杂度。通过比较这些不同启发式函数的性能,我们可以评估哪种方法在求解15数码问题时最有效。这种比较将有助于理解不同启发式函数对搜索算法效率的影响,从而为开发更高效的问题求解策略提供重要的洞见。如下面的代码所示:
1 | // 记录开始时间 |
实验结果
使用的不同方法及其特点
基于上述结果,我们可以得出每种方法的特点:
汉明距离(Hamming Distance):
- 特点:计算当前状态中与目标状态不匹配的方块数量。简单易计算,但不考虑实际步数,可能不够精确。
- 优点:实现简单,计算速度快。
- 缺点:对于更复杂的布局,可能无法提供足够有效的指导。
曼哈顿距离(Manhattan Distance):
- 特点:计算每个数字方块从其当前位置到目标位置的格子数总和。更准确地反映了方块的实际移动距离。
- 优点:相对准确,适用于大多数情况。
- 缺点:计算量比汉明距离大,可能导致搜索速度略慢。
线性冲突(Linear Conflict):
- 特点:在曼哈顿距离的基础上增加了额外的线性冲突考量,考虑了特定方块之间的相互影响。
- 优点:提供了更接近实际步数的估计,可以在某些情况下加速解的发现。
- 缺点:计算复杂度更高,对于一些简单布局可能是过度优化。
实验结果的展示
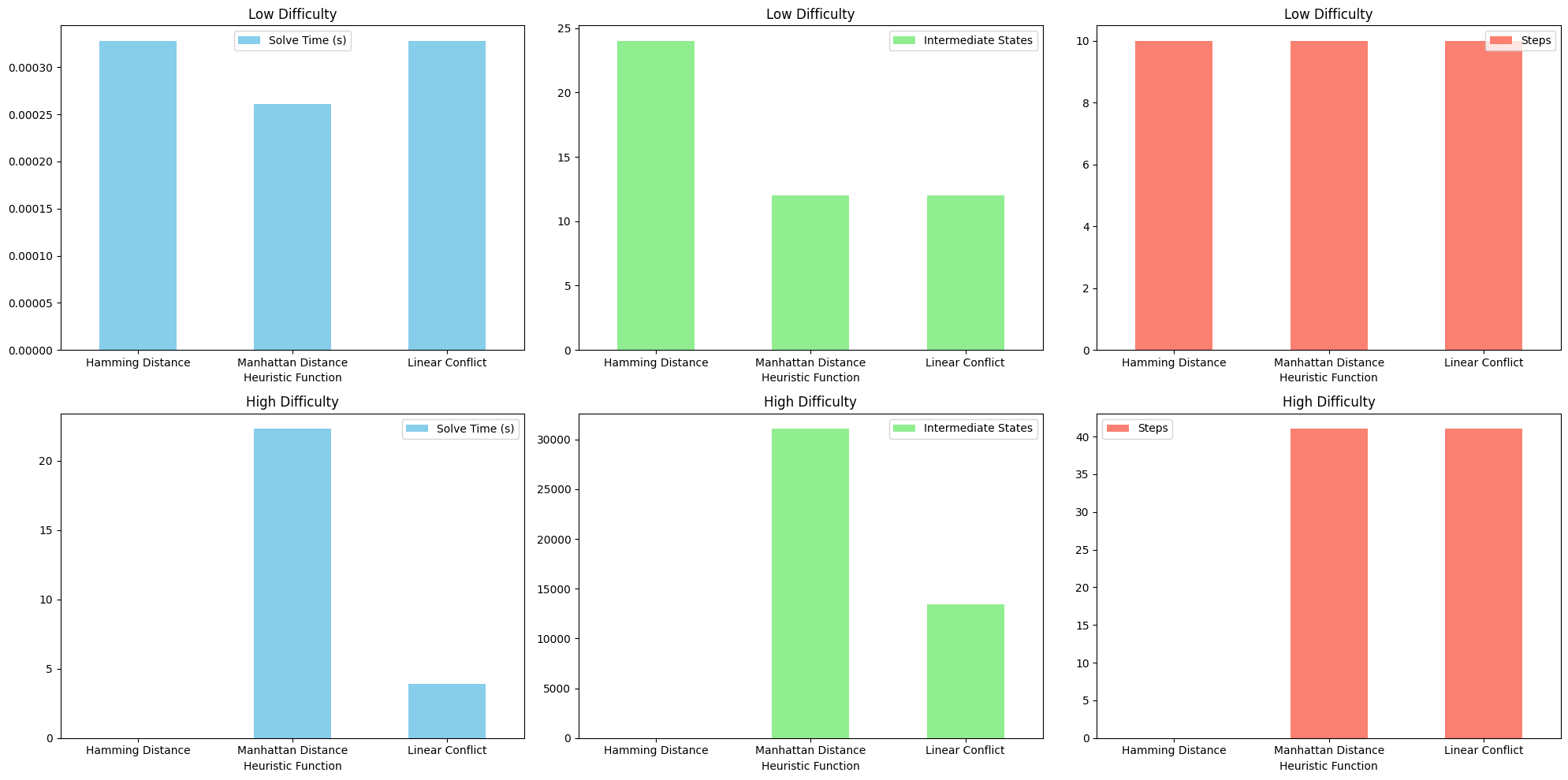
通过运行程序,我们得到了下面的结果运行结果,表4-1展示了不同方法在相同实例下的性能差异。通过对比求解时间和步数,可以看出哪种方法在特定情况下更加高效。例如,在实例1中,曼哈顿距离表现出了更短的求解时间和更少的步数;而在实例2中,线性冲突求解时间更短、步数更少,显示出其在更复杂的布局中的优势。
| 实例名称 | 求解时间 (秒) | 中间状态数 | 步数 | 启发函数 |
|---|---|---|---|---|
| 低难度实例 | 0.000327873 | 24 | 10 | 汉明距离 |
| 低难度实例 | 0.000260946 | 12 | 10 | 曼哈顿距离 |
| 低难度实例 | 0.000327643 | 12 | 10 | 线性冲突 |
| 高难度实例 | TLE | TLE | TLE | 汉明距离 |
| 高难度实例 | 22.2947 | 31056 | 41 | 曼哈顿距离 |
| 高难度实例 | 3.87911 | 13438 | 41 | 线性冲突 |
实验分析与讨论
性能比较
在实验中,我们对比了三种不同启发式函数(汉明距离、曼哈顿距离和线性冲突)在解决15数码问题时的性能表现。下面是对这些方法的性能比较和分析:
汉明距离:
- 在低难度实例中表现适中,但在高难度实例中无法在合理时间内找到解决方案(时间超限TLE)。
- 汉明距离作为一种简单的启发式函数,在处理复杂问题时效率较低。
曼哈顿距离:
- 在低难度实例中效率高,求解时间和中间状态数均优于汉明距离。
- 在高难度实例中能够找到解决方案,但求解时间较长,生成的中间状态数量多。
线性冲突:
- 在低难度实例中的表现与曼哈顿距离相似。
- 在高难度实例中表现最优,求解时间和中间状态数都显著优于其他方法。
定性和定量分析
定量分析:通过实验数据,我们可以看到,尤其在高难度实例中,线性冲突的求解时间和中间状态数明显低于曼哈顿距离和汉明距离。这表明线性冲突在处理复杂情况时更高效。
定性分析:汉明距离由于其简单性,在面对复杂情况时往往不足以提供有效的启发。曼哈顿距离,虽然比汉明距离更准确,但在处理特定的线性冲突情况时效率不高。线性冲突通过在曼哈顿距离的基础上增加额外的考量,能够更好地指导搜索过程,尤其是在复杂的实例中。
结果可视化
性能比较可视化
为了直观展示不同方法的性能差异,本实验使用条形图来表示求解时间和步数的比较。对于每种方法,使用一个条形图来表示不同实例下的求解时间,步数和中间状态数。这种可视化方法可以直观地显示出在不同复杂度的实例中,哪种方法更有效,以及它们在性能上的差异。
求解过程可视化
本实验的代码中通过宏定义DEBUG来打印中间过程的数据,便于展现求解过程中f值、g值和h值的变化,如下述代码所示:
1 | // 是否打印中间状态 |
输出如下:
1 | 5 1 3 4 2 0 7 8 10 6 11 12 9 13 14 15 |
结论
实验结果总结
本次实验对15数码问题的求解进行了深入的分析和比较,主要关注点在于不同启发式函数在A*搜索算法中的表现。实验结果显示:
不同启发式函数的表现:在低难度实例中,曼哈顿距离和线性冲突表现出接近的高效率,而汉明距离虽然能够解决问题,但效率稍低。在高难度实例中,汉明距离无法在合理时间内找到解决方案,而线性冲突在求解时间和生成的中间状态数量上均显著优于曼哈顿距离。
效率和复杂度:线性冲突由于其在曼哈顿距离的基础上增加了额外考虑因素,因此在处理更复杂的布局时更为高效。这表明复杂问题求解中,考虑更多因素的启发式函数可能更优。
改进思考与建议
启发式函数的优化:虽然线性冲突在本实验中表现最佳,但仍有进一步优化的空间。可以考虑开发新的启发式函数,或改进现有的函数,使其更精确地反映实际解决问题所需的步骤。
算法的混合使用:在不同阶段或不同类型的实例中,结合使用不同的启发式函数可能会提高效率。例如,对于简单实例使用曼哈顿距离,在达到一定复杂度后切换到线性冲突。
探索其他搜索算法:虽然A*算法在许多情况下有效,但探索其他搜索算法,如IDA*或双向搜索,可能在特定情况下更有效。
内存和处理优化:考虑到高难度实例中生成的大量中间状态,优化内存管理和处理效率是提高算法整体性能的关键。例如,可以采用更高效的数据结构或改进状态存储方法。
并行计算:考虑到15数码问题的计算密集性,利用并行计算资源(如多线程或分布式计算)可能会显著提高求解速度。
实际应用场景的适应性:考虑将这些算法应用于实际问题时的适应性,如机器人路径规划等,可能需要对算法进行相应的调整和优化。
总的来说,本实验提供了对15数码问题求解方法的深入理解,并指出了现有方法的优势和局限性。未来的工作应着重于进一步优化算法性能,同时探索新的算法和技术,以提高解决复杂问题的效率和准确性。
参考文献
[1] Korf, R. E. (1985). Depth-first iterative-deepening: An optimal admissible tree search. Artificial Intelligence, 27(1), 97-109.
[2] Hart, P. E., Nilsson, N. J., & Raphael, B. (1968). A formal basis for the heuristic determination of minimum cost paths. IEEE Transactions on Systems Science and Cybernetics, 4(2), 100-107.
[3] Manzini, G. (1995). BIDA*: An improved perimeter search algorithm. Artificial Intelligence, 75(2), 347-360.
[4] Felner, A., Korf, R. E., & Hanan, S. (2004). Additive pattern database heuristics. Journal of Artificial Intelligence Research, 22, 279-318.
[5] Edelkamp, S., & Schrödl, S. (2012). Heuristic Search: Theory and Applications. Elsevier.
附录
实验代码
a_star.cpp
求解十五数码问题的C++代码,仅使用C++的部分新特性,核心数据结构均为C语言实现。
1 |
|
plot.ipynb
绘制可视化图像的Python代码。
1 | import matplotlib.pyplot as plt |
实验数据表和图表
| 实例名称 | 求解时间 (秒) | 中间状态数 | 步数 | 启发函数 |
|---|---|---|---|---|
| 低难度实例 | 0.000327873 | 24 | 10 | 汉明距离 |
| 低难度实例 | 0.000260946 | 12 | 10 | 曼哈顿距离 |
| 低难度实例 | 0.000327643 | 12 | 10 | 线性冲突 |
| 高难度实例 | TLE | TLE | TLE | 汉明距离 |
| 高难度实例 | 22.2947 | 31056 | 41 | 曼哈顿距离 |
| 高难度实例 | 3.87911 | 13438 | 41 | 线性冲突 |

遗传算法求最值问题实验报告
遗传算法的基本原理
遗传算法是一种模拟达尔文生物进化论的自然选择和遗传学原理的优化算法。其基本原理归纳如下:
- 编码:在遗传算法开始之前,问题的解决方案被编码成一定长度的染色体,通常是二进制字符串。
- 初始群体:算法随机生成一个初始种群,这个种群由多个染色体(即潜在的解决方案)组成。
- 适应度函数:定义一个适应度函数来评价种群中每个个体的适应度,即它们的解决问题的能力。适应度越高的个体被认为是越好的解决方案。
- 选择:根据个体的适应度进行选择。适应度高的个体更有可能被选中用于下一代的繁殖。
- 交叉:模拟生物的杂交过程,交叉是遗传算法中的一种重要操作。它通过混合两个父代染色体的基因来产生新的后代。
- 变异:通过随机改变个体染色体中的一个或多个基因来引入新的遗传材料,保证种群不会陷入局部最优解。
- 新一代:通过选择、交叉和变异生成的新个体构成新的种群。这个过程会不断重复,种群会逐渐向更优解进化。
- 终止条件:算法继续迭代直到满足特定的终止条件,如达到最大迭代次数、适应度达到要求的阈值或适应度长时间未改善等。
遗传算法利用了自然选择的“优胜劣汰”原理和基因的交叉与变异原理,使得种群能够不断进化,最终趋向于最优解。这种基于群体的搜索策略有效地平衡了解空间的全局搜索和局部探索能力,因而能够在各种复杂的优化问题中找到高质量的解。
遗传算法的流程图图下图所示:
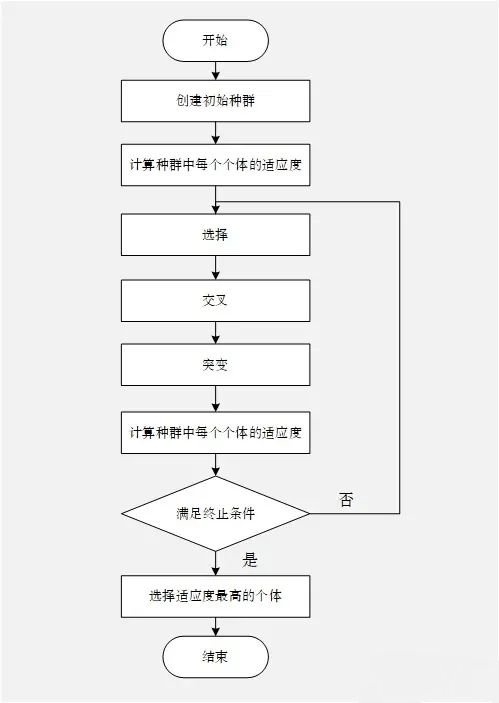
遗传算法的伪代码如下所示:
1 | 1. 初始化参数: |
初始值的设置对结果的影响
问题一:哪些影响
在遗传算法中,交叉概率和变异概率是两个核心参数,它们对算法的性能和求解过程产生深远影响。下面分别讨论这两个参数的影响:
- 交叉概率(Crossover Probability):
- 高交叉概率
- 促进基因多样性:高交叉概率意味着种群中的个体有更多机会与其他个体交换基因,这有助于在种群中创造出更多的基因多样性。
- 加速收敛:由于基因的广泛交换,算法可能更快地找到问题的优化区域,从而加速解决方案的收敛。
- 破坏优秀解:同时,过高的交叉概率可能导致优秀个体的优质基因被破坏,因为太频繁的基因重组可能会分解良好的基因组合。
- 低交叉概率
- 缓慢进化:如果交叉概率太低,新的个体可能就是父代的近乎完全复制品,这会限制种群的进化速度。
- 降低多样性:基因交换的减少可能导致种群多样性的降低,增加早熟收敛到局部最优解的风险。
- 高交叉概率
- 变异概率(Mutation Probability):
- 高变异概率
- 增加多样性:变异是引入新特征的主要方式,高变异率可以增加种群的遗传多样性,有助于算法跳出局部最优。
- 防止早熟收敛:通过引入新的基因变体,高变异率可以帮助防止算法过早收敛到非最优解。
- 过度随机化:然而,过高的变异率可能导致种群过于随机,解决方案可能在搜索空间中随机漫游,而无法有效地收敛。
- 低变异概率
- 稳定性:低变异率可以帮助维持优秀个体的基因,减少优质解被破坏的风险。
- 可能的早熟收敛:如果变异率太低,可能不足以防止算法陷入局部最优解,特别是在解决复杂或具有众多局部最优的问题时。
- 高变异概率
综上所述,交叉概率和变异概率需要根据问题的特性和算法的实际表现进行仔细调整。没有一种通用的最佳设置,它们的最佳值通常是通过实验和问题分析得出的。过高或过低的这些参数都可能妨碍遗传算法找到一个有效的全局最优解。在实践中,经常需要进行多次试验和调整,以找到特定问题的最佳参数设置,详见问题二的叙述。
问题二:如何设置
在使用遗传算法进行求解时,正确设置交叉概率和变异概率是至关重要的,因为它们直接影响到算法的搜索能力和收敛性能。以下是一些指导原则和方法,可以帮助你设置这些参数:
- 经验设置:
- 交叉概率: 通常,交叉概率被设置为相对较高的值,例如0.6至0.9,以促进有用基因的传播和种群多样性的保持。
- 变异概率: 变异概率通常设置得较低,例如0.01至0.1,因为过高的变异率可能导致过度探索和算法收敛的随机性。
- 问题相关性:
- 了解你要解决问题的性质很重要。对于一些复杂的问题,可能需要更高的变异率来避免局部最优。而对于一些相对简单或者解空间平滑的问题,较高的交叉率和较低的变异率可能更适合。
- 适应性方法:
- 一些高级的遗传算法使用自适应方法来动态调整交叉和变异率,这基于当前种群的表现。例如,如果种群的多样性下降,算法可能会自动增加变异率。
- 实验调优:
- 参数设置通常需要多次实验来确定。通过观察算法在不同参数设置下的表现,你可以逐渐调整它们以获得最佳表现。设计实验时,可以使用参数敏感性分析、网格搜索或贝叶斯优化方法。
- 参考文献:
- 查看相关研究和文献来了解类似问题上成功应用的参数设置。通过学习先前的研究,你可以获得关于可能的最佳参数范围的初始见解。
- 使用启发式规则:
- 一些研究提出了启发式规则来设置参数,例如,当种群规模较大时,可能需要较低的交叉和变异率,因为大的种群本身就提供了更多的多样性。
- 并行试验:
- 如果资源允许,可以并行运行多个算法实例,每个实例使用不同的参数组合。在一系列运行后,选择表现最佳的参数组合。
需要注意的是,不存在一种通用的“最佳”设置,因为最有效的参数设置取决于特定的问题和算法实现。因此,通常需要通过实验来确定适用于特定问题的最佳参数配置。同时,参数设置不仅仅是一个一次性的过程,而是一个持续的过程,可能需要根据算法的长期表现进行调整。
Python代码实现
Python代码的编写使用Jupyter Notebook进行,所以在报告中进行分段展示。
1 | import numpy as np |
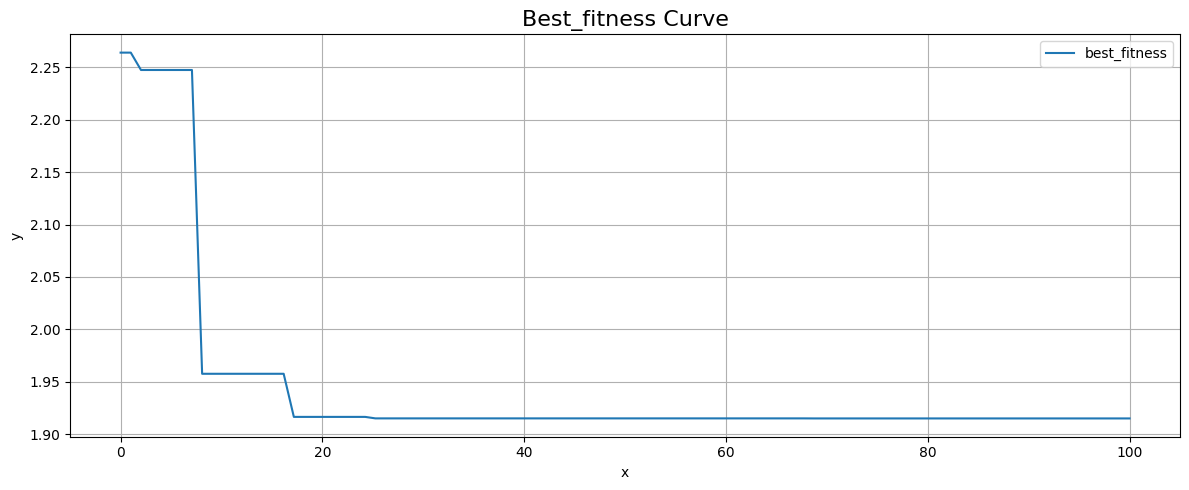
1 | # 最佳个体曲线 |
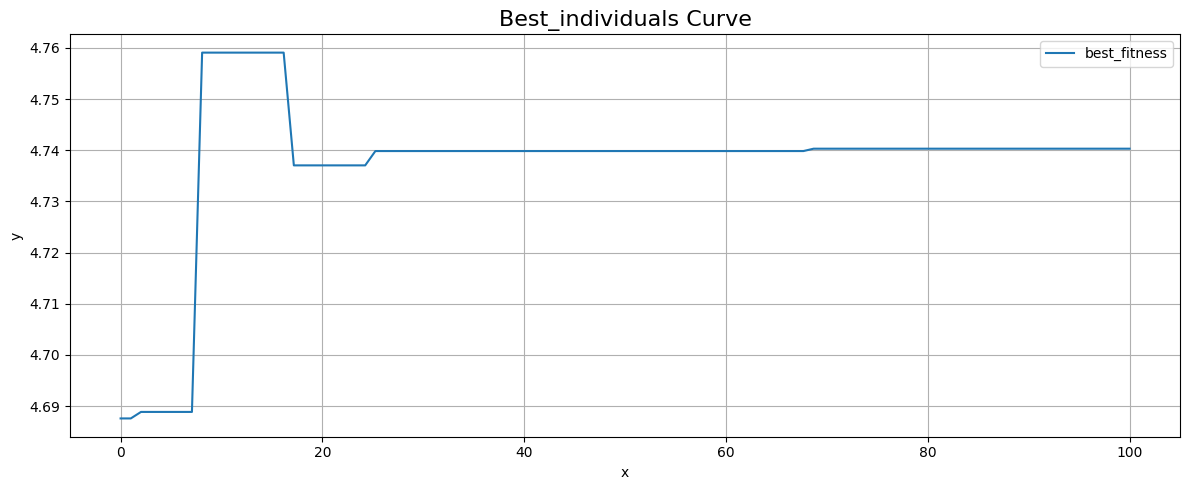
1 | # 结果 |
Console输出:
1 | (1.9151576579498766, 4.741060612805114) |
1 | # 可视化 |










